Ciphertext indistinguishability
Ciphertext indistinguishability is a property of many encryption schemes. Intuitively, if a cryptosystem possesses the property of indistinguishability, then an adversary will be unable to distinguish pairs of ciphertexts based on the message they encrypt. The property of indistinguishability under chosen plaintext attack is considered a basic requirement for most provably secure public key cryptosystems, though some schemes also provide indistinguishability under chosen ciphertext attack and adaptive chosen ciphertext attack. Indistinguishability under chosen plaintext attack is equivalent to the property of semantic security, and many cryptographic proofs use these definitions interchangeably.
A cryptosystem is considered secure in terms of indistinguishability if no adversary, given an encryption of a message randomly chosen from a two-element message space determined by the adversary, can identify the message choice with probability significantly better than that of random guessing (1/2). If any adversary can succeed in distinguishing the chosen ciphertext with a probability significantly greater than 1/2, then this adversary is considered to have an "advantage" in distinguishing the ciphertext, and the scheme is not considered secure in terms of indistinguishability. This definition encompasses the notion that in a secure scheme, the adversary should glean no information from seeing a ciphertext. Therefore, the adversary should be able to do no better than if it guessed randomly.
Contents |
Formal definitions
Security in terms of indistinguishability has many definitions, depending on assumptions made about the capabilities of the attacker. It is normally presented as a game, where the cryptosystem is considered secure if no adversary can win the game with significantly greater probability than an adversary who must guess randomly. The most common definitions used in cryptography are indistinguishability under chosen plaintext attack (abbreviated IND-CPA), indistinguishability under (non-adaptive) chosen ciphertext attack (IND-CCA), and indistinguishability under adaptive chosen ciphertext attack (IND-CCA2). Security under either of the latter definition implies security under the previous ones: a scheme which is IND-CCA secure is also IND-CPA secure, and a scheme which is IND-CCA2 secure is both IND-CCA and IND-CPA secure. Thus, IND-CCA2 is the strongest of the three definitions of security.
Indistinguishability under chosen-plaintext attack (IND-CPA)
For a probabilistic asymmetric key encryption algorithm, indistinguishability under chosen plaintext attack (IND-CPA) is defined by the following game between an adversary and a challenger. For schemes based on computational security, the adversary is modeled by a probabilistic polynomial time Turing machine, meaning that it must complete the game and output a guess within a polynomial number of time steps. In this definition E(PK, M) represents the encryption of a message M under the key PK:
- The challenger generates a key pair PK, SK based on some security parameter k (e.g., a key size in bits), and publishes PK to the adversary. The challenger retains SK.
- The adversary may perform any number of encryptions or other operations.
- Eventually, the adversary submits two distinct chosen plaintexts
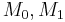 to the challenger.
to the challenger. - The challenger selects a bit b
 {0, 1} uniformly at random, and sends the challenge ciphertext C = E(PK,
{0, 1} uniformly at random, and sends the challenge ciphertext C = E(PK, 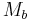 ) back to the adversary.
) back to the adversary. - The adversary is free to perform any number of additional computations or encryptions. Finally, it outputs a guess for the value of b.
A cryptosystem is indistinguishable under chosen plaintext attack if every probabilistic polynomial time adversary has only a negligible "advantage" over random guessing. An adversary is said to have a negligible "advantage" if it wins the above game with probability 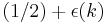 , where
, where 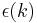 is a negligible function in the security parameter k, that is for every (nonzero) polynomial function
is a negligible function in the security parameter k, that is for every (nonzero) polynomial function  there exists
there exists 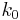 such that
such that 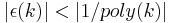 for all
for all 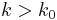 .
.
Although the adversary knows 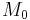 ,
, 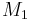 and PK, the probabilistic nature of E means that the encryption of
and PK, the probabilistic nature of E means that the encryption of 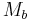 will be only one of many valid ciphertexts, and therefore encrypting
will be only one of many valid ciphertexts, and therefore encrypting 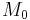 ,
, 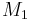 and comparing the resulting ciphertexts with the challenge ciphertext does not afford any non-negligible advantage to the adversary.
and comparing the resulting ciphertexts with the challenge ciphertext does not afford any non-negligible advantage to the adversary.
While the above definition is specific to an asymmetric key cryptosystem, it can be adapted to the symmetric case by replacing the public key encryption function with an "encryption oracle", which retains the secret encryption key and encrypts arbitrary plaintexts at the adversary's request.
Indistinguishability under chosen ciphertext attack/adaptive chosen ciphertext attack (IND-CCA, IND-CCA2)
Indistinguishability under non-adaptive and adaptive Chosen Ciphertext Attack (IND-CCA, IND-CCA2) uses a definition similar to that of IND-CPA. However, in addition to the public key (or encryption oracle, in the symmetric case), the adversary is given access to a "decryption oracle" which decrypts arbitrary ciphertexts at the adversary's request, returning the plaintext. In the non-adaptive definition, the adversary is allowed to query this oracle only up until it receives the challenge ciphertext. In the adaptive definition, the adversary may continue to query the decryption oracle even after it has received a challenge ciphertext, with the caveat that it may not pass the challenge ciphertext for decryption (otherwise, the definition would be trivial).
- The challenger generates a key pair PK, SK based on some security parameter k (e.g., a key size in bits), and publishes PK to the adversary. The challenger retains SK.
- The adversary may perform any number of encryptions, calls to the decryption oracle based on arbitrary ciphertexts, or other operations.
- Eventually, the adversary submits two distinct chosen plaintexts
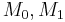 to the challenger.
to the challenger. - The challenger selects a bit b ∈ {0, 1} uniformly at random, and sends the "challenge" ciphertext C = E(PK,
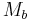 ) back to the adversary.
) back to the adversary. - The adversary is free to perform any number of additional computations or encryptions.
- In the non-adaptive case (IND-CCA), the adversary may not make further calls to the decryption oracle.
- In the adaptive case (IND-CCA2), the adversary may make further calls to the decryption oracle, but may not submit the challenge ciphertext C.
- Finally, the adversary outputs a guess for the value of b.
A scheme is IND-CCA/IND-CCA2 secure if no adversary has a non-negligible advantage in winning the above game.
Equivalences and implications
Indistinguishability is an important property for maintaining the confidentiality of encrypted communications. However, the property of indistinguishability has in some cases been found to imply other, apparently unrelated security properties. Sometimes these implications go in both directions, making two definitions equivalent; for example, it is known that the property of indistinguishability under adaptive chosen ciphertext attack (IND-CCA2) is equivalent to the property of non-malleability under the same attack scenario (NM-CCA2). This equivalence is not immediately obvious, as non-malleability is a property dealing with message integrity, rather than confidentiality. In other cases, it has been demonstrated that indistinguishability can be combined with certain other definitions, in order to imply still other useful definitions, and vice versa. The following list summarizes a few known implications, though it is by no means complete.
The notation 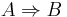 means that property A implies property B.
means that property A implies property B. 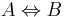 means that properties A and B are equivalent.
means that properties A and B are equivalent. 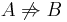 means that property A does not necessarily imply property B.
means that property A does not necessarily imply property B.
- IND-CPA
 semantic security under CPA.
semantic security under CPA. - NM-CPA (non-malleability under chosen plaintext attack)
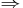 IND-CPA.
IND-CPA. - NM-CPA (non-malleability under chosen plaintext attack)
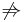 IND-CCA2.
IND-CCA2. - NM-CCA2 (non-malleability under adaptive chosen ciphertext attack)
 IND-CCA2.
IND-CCA2.
Literature
- Jonathan Katz, Yehuda Lindell, "Introduction to Modern Cryptography: Principles and Protocols," Chapman & Hall/CRC, 2007
See also
|
||||||||||