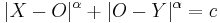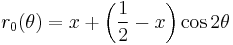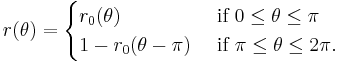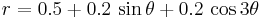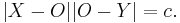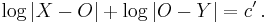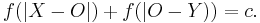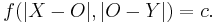Chordal problem

In the book^[1] there is a generalization of the equichordal point problem attributed to R. Gardner.

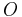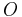We consider a point $O$ inside a Jordan curve with the property that for any chord $[X,Y]$ of the curve passing through $O$ the two parts $[X,O]$ and $[O,Y]$ of the chord satisfy the following equation, where $\alpha$ is a fixed real number:

$|X-O|^\alpha%2B|O-Y|^\alpha = c$ ^[2]

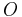where $c$ is a constant not depending on the chord. In this article we will call a point $O$ satisfying equation^[2] a chordal point, or $\alpha$ -chordal point.

The template for all chordal problems is this:

Problem: Is there a curve with two or more distinct points with this property?

1 Curves with one equichordal point
2 An example
3 Special cases
4 The status of various special cases
5 See also
6 References

Curves with one equichordal point

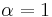The center of the circle is a solution of the chordal equation^[2] for an arbitrary $\alpha$ . One can show a continuum of solutions for many $\alpha$ , for example, $\alpha=1$ . The method of construction such solutions is by writing the equation of the curve in the form 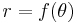$r = f(\theta)$ in polar coordinates. For 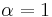$\alpha=1$ , the solution may be found in this article.^[3]

An example

This is an example of a curve with one equichordal point. based on an example in.^[4] The core idea is that we may start with any Jordan arc given in polar coordinates by an equation 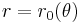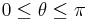$r=r_0(\theta)$ , $0\leq\theta\leq\pi$ , and complement it to a closed Jordan curve given by the equation 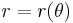$r=r(\theta)$ for all $\theta\in[0,2\pi]$ . Along the way, we must satisfy some number of conditions to ensure continuity of the resulting curve.

Let us define a function 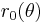$r_0(\theta)$ by the formula:

$r_0(\theta) = x%2B\left(\frac{1}{2}-x\right)\cos2\theta$

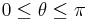where $x$ is a real parameter and $x\in(1/4,1/2]$ . This function is clearly defined for all real $\theta$ , but we only use its values for $0\leq\theta\leq\pi$ . Clearly, $r(0)= r(\pi)$ .

We define the second function 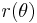$r(\theta)$ by the formula:

$r(\theta) = \begin{cases} r_0(\theta)&\text{ if }0\leq\theta\leq\pi\\ 1-r_0(\theta-\pi)&\text{ if }\pi\leq\theta\leq2\pi. \end{cases}$

This function has the following properties:

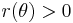$r(\theta)>0$ ;
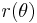$r(\theta)$ is continuous on $[0,2\pi]$ ;
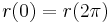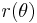$r(0)=r(2\pi)$ , so $r(\theta)$ extends uniquely to a 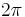$2\pi$ -periodic, continuous function on 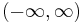$(-\infty,\infty)$ ; from now on, we identify $r$ with this extension;
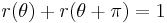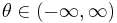$r(\theta)%2Br(\theta%2B\pi) = 1$ for all $\theta\in(-\infty,\infty)$ .

These properties imply that the curve given in polar coordinates by the equation 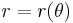$r=r(\theta)$ is a closed Jordan curve and that the origin is an equichordal point.

The construction presented here and based on^[4] results in a curve which is 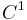$C^1$ but not 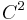$C^2$ , with the exception of 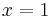$x=1$ , when the curve becomes a circle. Rychlik^[3] formulated conditions on the Fourier series of 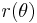$r(\theta)$ which easily allow constructing of curves with one equichordal point, including analytic curves. Rychlik gives a specific example of an analytic curve:

$r = 0.5%2B0.2\,\sin\theta %2B 0.2\,\cos3\theta$

Fourier series analysis in Rychlik's paper^[3] reveals the pattern of Fourier coefficients of all suitable functions 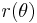$r(\theta)$ .

Special cases

For 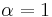$\alpha=1$ we obtain the equichordal point problem, and for 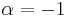$\alpha=-1$ we obtain the equireciprocal point problem considered by Klee.^[5]^[6]

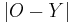We may also consider a more general relationship between $|X-O|$ and $|O-Y|$ . For example, the equiproduct point problem is obtained by considering the equation:

$|X-O||O-Y|=c. \,$

Equivalently,

$\log|X-O| %2B \log|O-Y| = c'\,.$

This naturally leads to a more general class of problems. For a given function 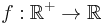$f:\mathbb{R}^%2B\to\mathbb{R}$ we may study the equations:

$f(|X-O|) %2B f(|O-Y)) = c .$

Even more generally, we could consider a function 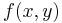$f(x,y)$ of two real variables. We need to assume that $f$ is symmetric, i.e. $f(x,y)=f(y,x)$ . Then we may consider the equation:

$f(|X-O|, |O-Y|) = c.$

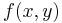Clearly, $f(x,y)$ needs only be defined for positive $x$ and $y$ . Thus, the family of chordal problems of this type is parameterized by symmetric functions of two variables.

The status of various special cases

The equichordal point problem (α = 1)

This has been the most famous of the chordal problems. In this case, the equation^[2] states that every chord passing through 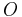$O$ has the same length. It has become known as the equichordal point problem, and was fully solved in 1996 by Marek Rychlik.

The equireciprocal point problem (α = −1)

Klee^[5] proved that the ellipse solves the equireciprocal point problem, with the ellipse foci serving as the two equireciprocal points. However, in addition to the ellipses, many solutions of low smoothness also exist, as it was shown in.^[6] From the point of view of the equichordal point problem, this is due to the lack of hyperbolicity of the fixed points of a certain map of the plane.

Other cases

The method used in Rychlik's proof for the equichordal point problem may only generalize to some rational values of $\alpha$ . A reasonable conjecture could be:

Conjecture: There are no solutions of the Chordal Problem for rational $\alpha$ close to 1.

References

^ H. Croft, K. J. Falconer, and R. K. Guy. Unsolved Problems in Geometry, volume II of 'Problem Books in Mathematics'. Springer-Verlag, New York, Berlin, 1991.
^ ^a ^b ^c ^d The Chordal Equation
^ ^a ^b ^c Marek Rychlik, The Equichordal Point Problem, Electronic Research Announcements of the AMS, 1996, pages 108-123, available on-line at [1]
^ ^a ^b http://mathworld.wolfram.com/EquichordalPoint.html
^ ^a ^b V. Klee. Can a plane convex body have two equireciprocal points? American Mathematical Monthly, 76:54–55, 1969, correction in 78:1114, 1971
^ ^a ^b K. J. Falconer. On the equireciprocal point problem. Geom. Dedicata, 14:113–126, 1983