Chase (algorithm)
The Chase is a simple fixpoint algorithm testing and enforcing implication of data dependencies in database systems. It plays important roles in database theory as well as in practice. It is used, directly or indirectly, on an everyday basis by people who design databases, and it is used in commercial systems to reason about the consistency and correctness of a data design. New applications of the chase in meta-data management and data exchange are still being discovered.
The Chase has its origins in two seminal papers, one by David Maier, Alberto O. Mendelzon, and Yehoshua Sagiv[1] and the other by Alfred V. Aho, Catriel Beeri, and Jeffrey D. Ullman[2].
Chase test is for testing whether the projection of a relation onto any decomposition can be recovered by rejoining. Let t be a tuple in 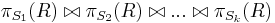 where R is a relation and F is a set of functional dependencies (FD). If tuples in R are represented as t1, ..., tk, the join of the projections of each ti should agree with t on
where R is a relation and F is a set of functional dependencies (FD). If tuples in R are represented as t1, ..., tk, the join of the projections of each ti should agree with t on 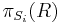 where i = 1, 2, ..., k. If ti is not on
where i = 1, 2, ..., k. If ti is not on 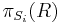 , the value is unknown.
, the value is unknown.
Chase test can be done by drawing a tableau. Suppose R has attributes A, B, ... and components of t are a, b, .... For ti use the same letter as t in the components that are in Si but subscript the letter with i if the component is not in i. Then, ti will agree with t if it is in Si and will have a unique value otherwise.
Example
Suppose R(A, B, C, D) which are decomposed into relations with attributes S1 = {A, D}, S2 = {A, C} and S3 = {B, C, D} and F = {A→B, B→C, CD→A} is given. The initial tableau for this decomposition is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c1 | d |
| a | b2 | c | d2 |
| a3 | b | c | d |
The first row represents S1. The components for attributes A and D are unsubscripted and those for attributes B and C are subscripted with i = 1. The second and third rows are filled in the same manner with S2 and S3 respectively. The goal for this test is to use the given F to prove that t = (a, b, c, d) is really in R. To do so, the tableau can be chased by applying the FD’s in F to equate symbols in the tableau. Final tableau with a row that is the same as t implies that any tuple t in the join of the projections is actually a tuple of R. To perform the chase test, first decompose all FD’s in F so each FD has a single attribute on the right hand side of the "arrow". F remains unchanged because all of its FD's already has a single attribute on the right hand side. F = {A→B, B→C, CD→A}. When equating two symbols, if one of them is unsubscripted, make the other be the same so that the final tableau can have a row that is exactly the same as t = (a, b, c, d). Also, if both have their own subscript, change either to be the other. However, to avoid confusion, all of the occurrences should be changed. First, apply A→B to the tableau. The first row is (a, b1, c1, d) where a is unsubscripted and b1 is subscripted with 1. Comparing the first row with the second one, change b2 to b1. Since the third row has a3, b in the third row stays the same. The resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c1 | d |
| a | b1 | c | d2 |
| a3 | b | c | d |
Then consider B→C. Both first and second rows have b1 and notice that the second row has an unsubscripted c. Therefore, the first row changes to (a, b1, c, d). Then the resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c | d |
| a | b1 | c | d2 |
| a3 | b | c | d |
Now consider CD→A. The first row has an unsubscripted c and an unsubscripted d, which is the same as in third row. This means that the A value for row one and three must be the same as well. Hence, change a3 in the third row to a. The resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c | d |
| a | b1 | c | d2 |
| a | b | c | d |
At this point, notice that the third row is (a, b, c, d) which is the same as t. Therefore, this is the final tableau for the chase test with given R and F. Hence, whenever R is projected onto S1, S2 and S3 and rejoined, the result is in R. Particularly, the resulting tuple is the same as the tuple of R that is projected onto {B, C, D}.
References
- ^ David Maier, Alberto O. Mendelzon, and Yehoshua Sagiv: "Testing Implications of Data Dependencies". ACM Trans. Datab. Syst. 4(4):455-469, 1979.
- ^ Alfred V. Aho, Catriel Beeri, and Jeffrey D. Ullman: "The Theory of Joins in Relational Databases", ACM Trans. Datab. Syst. 4(3):297-314, 1979.
- Serge Abiteboul, Richard B. Hull, Victor Vianu: Foundations of Databases. Addison-Wesley, 1995.
- A. V. Aho, C. Beeri, and J. D. Ullman: The Theory of Joins in Relational Databases. ACM Transactions on Database Systems 4(3): 297-314, 1979.
- J. D. Ullman: Principles of Database and Knowledge-Base Systems, Volume I. Computer Science Press, New York, 1988.
- J. D. Ullman, J. Widom: A First Course in Database Systems (3rd ed.). pp. 96–99. Pearson Prentice Hall, 2008.