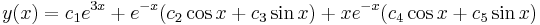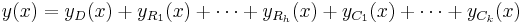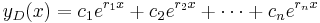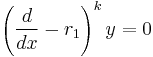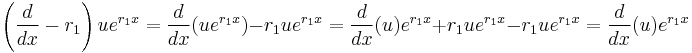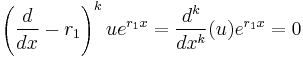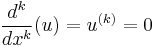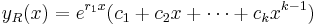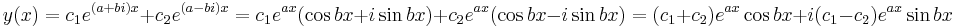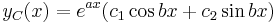Characteristic equation (calculus)
In mathematics, the characteristic equation (or auxiliary equation[1]) is an algebraic equation of degree 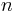 on which depends the solutions of a given
on which depends the solutions of a given 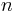 th-order differential equation.[2] The characteristic equation can only be formed when the differential equation is linear, homogeneous, and has constant coefficients.[1] Such a differential equation, with
th-order differential equation.[2] The characteristic equation can only be formed when the differential equation is linear, homogeneous, and has constant coefficients.[1] Such a differential equation, with 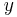 as the dependent variable and
as the dependent variable and 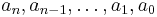 as constants,
as constants,
will have a characteristic equation of the form
where 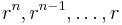 are the roots from which the general solution can be formed.[1][3][4] This method of integrating linear ordinary differential equations with constant coefficients was discovered by Leonhard Euler, who found that the solutions depended on an algebraic 'characteristic' equation.[2] The qualities of the Euler's characteristic equation were later considered in greater detail by French mathematicians Augustin-Louis Cauchy and Gaspard Monge.[2][4]
are the roots from which the general solution can be formed.[1][3][4] This method of integrating linear ordinary differential equations with constant coefficients was discovered by Leonhard Euler, who found that the solutions depended on an algebraic 'characteristic' equation.[2] The qualities of the Euler's characteristic equation were later considered in greater detail by French mathematicians Augustin-Louis Cauchy and Gaspard Monge.[2][4]
Contents |
Derivation
Starting with a linear homogeneous differential equation with constant coefficients 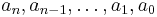 ,
,
it can be seen that if 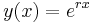 , each term would be a constant multiple of
, each term would be a constant multiple of 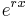 . This results from the fact that the derivative of the exponential function
. This results from the fact that the derivative of the exponential function 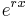 is a multiple of itself. Therefore,
is a multiple of itself. Therefore, 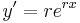 ,
, 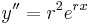 , and
, and 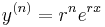 are all multiples. This suggests that certain values of
are all multiples. This suggests that certain values of 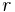 will allow multiples of
will allow multiples of 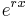 to sum to zero, thus solving the homogeneous differential equation.[3] In order to solve for
to sum to zero, thus solving the homogeneous differential equation.[3] In order to solve for 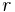 , one can substitute
, one can substitute 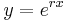 and its derivatives into the differential equation to get
and its derivatives into the differential equation to get
Since 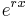 can never equate to zero, it can be divided out, giving the characteristic equation
can never equate to zero, it can be divided out, giving the characteristic equation
By solving for the roots, 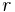 , in this characteristic equation, one can find the general solution to the differential equation.[1][4] For example, if
, in this characteristic equation, one can find the general solution to the differential equation.[1][4] For example, if 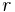 is found to equal to 3, then the general solution will be
is found to equal to 3, then the general solution will be 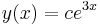 , where
, where 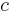 is a constant.
is a constant.
Formation of the general solution
| Example |
|---|
|
The linear homogeneous differential equation with constant coefficients has the characteristic equation By factoring the characteristic equation into one can see that the solutions for |
Solving the characteristic equation for its roots,  , allows one to find the general solution of the differential equation. The roots may be real and/or complex, as well as distinct and/or repeated. If a characteristic equation has parts with distinct real roots,
, allows one to find the general solution of the differential equation. The roots may be real and/or complex, as well as distinct and/or repeated. If a characteristic equation has parts with distinct real roots, 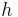 repeated roots, and/or
repeated roots, and/or 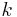 complex roots corresponding to general solutions of
complex roots corresponding to general solutions of 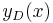 ,
,  , and
, and  , respectively, then the general solution to the differential equation is
, respectively, then the general solution to the differential equation is
Distinct real roots
The superposition principle for linear homogeneous differential equations with constant coefficients says that if  are
are 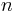 linearly independent solutions to a particular differential equation, then
linearly independent solutions to a particular differential equation, then  is also a solution for all values
is also a solution for all values  .[1][5] Therefore, if the characteristic equation has distinct real roots
.[1][5] Therefore, if the characteristic equation has distinct real roots  , then a general solution will be of the form
, then a general solution will be of the form
Repeated real roots
If the characteristic equation has a root 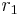 that is repeated
that is repeated 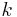 times, then it is clear that
times, then it is clear that 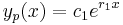 is at least one solution.[1] However, this solution lacks linearly independent solutions from the other
is at least one solution.[1] However, this solution lacks linearly independent solutions from the other 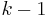 roots. Since
roots. Since 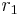 has multiplicity
has multiplicity 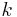 , the differential equation can be factored into[1]
, the differential equation can be factored into[1]
The fact that 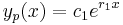 is one solution allows one to presume that the general solution may be of the form
is one solution allows one to presume that the general solution may be of the form 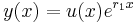 , where
, where 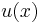 is a function to be determined. Substituting
is a function to be determined. Substituting 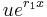 gives
gives
when 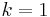 . By applying this fact
. By applying this fact 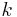 times, it follows that
times, it follows that
By dividing out 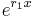 , it can be seen that
, it can be seen that
However, this is the case if and only if 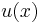 is a polynomial of degree
is a polynomial of degree 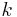 , so that
, so that 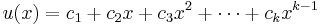 .[4] Since
.[4] Since 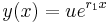 , the part of the general solution corresponding to
, the part of the general solution corresponding to 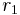 is
is
Complex roots
If the characteristic equation has complex roots of the form 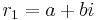 and
and 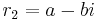 , then the general solution is accordingly
, then the general solution is accordingly 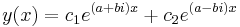 . However, by Euler's formula, which states that
. However, by Euler's formula, which states that 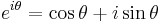 , this solution can be rewritten as follows:
, this solution can be rewritten as follows:
where 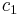 and
and 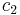 are constants that can be complex.[4] Note that if
are constants that can be complex.[4] Note that if 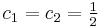 , then the particular solution
, then the particular solution 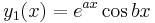 is formed. Similarly, if
is formed. Similarly, if 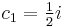 and
and 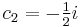 , then the independent solution formed is
, then the independent solution formed is 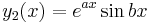 . Thus by the superposition principle for linear homogeneous differential equations with constant coefficients, the following general solution results for the part of a differential equation having complex roots
. Thus by the superposition principle for linear homogeneous differential equations with constant coefficients, the following general solution results for the part of a differential equation having complex roots 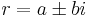
References
- ^ a b c d e f g Edwards, C. Henry; David E. Penney. "3". Differential Equations: Computing and Modeling. David Calvis. Upper Saddle River, New Jersey: Pearson Education. pp. 156–170. ISBN 978-0-13-600438-7.
- ^ a b c Smith, David Eugene. "History of Modern Mathematics: Differential Equations". University of South Florida. http://etc.usf.edu/lit2go/contents/2800/2892/2892_txt.html. Retrieved 2 March 2011.
- ^ a b Chu, Herman; Gaurav Shah, Tom Macall. "Linear Homogeneous Ordinary Differential Equations with Constant Coefficients". eFunda. http://www.efunda.com/math/ode/linearode_consthomo.cfm. Retrieved 1 March 2011.
- ^ a b c d e Cohen, Abraham (1906). An Elementary Treatise on Differential Equations. D. C. Heath and Company.
- ^ Dawkins, Paul. "Differential Equation Terminology". Paul's Online Math Notes. http://tutorial.math.lamar.edu/Classes/DE/PDETerminology.aspx. Retrieved 2 March 2011.
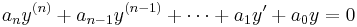
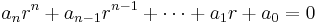
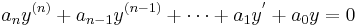
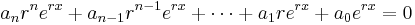
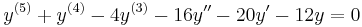
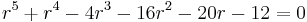
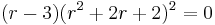
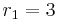 and the double complex root
and the double complex root 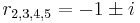 . This corresponds to the real-valued general solution with constants
. This corresponds to the real-valued general solution with constants  of
of