Character group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory. Whenever a group is represented by matrices, the function defined by the trace of the matrices is called a character; however, these traces do not in general form a group. Some important properties of these one-dimensional characters apply to characters in general:
- Characters are invariant on conjugacy classes.
- The characters of irreducible representations are orthogonal.
The primary importance of the character group for finite abelian groups is in number theory, where it is used to construct Dirichlet characters. The character group of the cyclic group also appears in the theory of the discrete Fourier transform. For locally compact abelian groups, the character group (with an assumption of continuity) is central to Fourier analysis.
Contents |
Preliminaries
Let G be an abelian group. A function 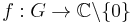 mapping the group to the non-zero complex numbers is called a character of G if it is a group homomorphism—that is, if
mapping the group to the non-zero complex numbers is called a character of G if it is a group homomorphism—that is, if 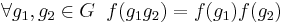 and
and 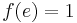 where e is the identity of the group.
where e is the identity of the group.
If f is a character of a finite group G, then each function value f(g) is a root of unity (since all elements of a finite group have finite order).
Each character f is a constant on conjugacy classes of G, that is, f(h g h−1) = f(g). For this reason, the character is sometimes called the class function.
A finite abelian group of order n has exactly n distinct characters. These are denoted by f1, ..., fn. The function f1 is the trivial representation; that is, 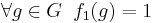 . It is called the principal character of G; the others are called the non-principal characters. The non-principal characters have the property that
. It is called the principal character of G; the others are called the non-principal characters. The non-principal characters have the property that 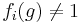 for some
for some 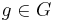 .
.
Definition
If G is an abelian group of order n, then the set of characters fk forms an abelian group under multiplication 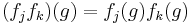 for each element
for each element 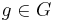 . This group is the character group of G and is sometimes denoted as
. This group is the character group of G and is sometimes denoted as 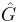 . It is of order n. The identity element of
. It is of order n. The identity element of 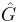 is the principal character f1. The inverse of fk is the reciprocal 1/fk. Note that since
is the principal character f1. The inverse of fk is the reciprocal 1/fk. Note that since 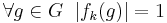 , the inverse is equal to the complex conjugate.
, the inverse is equal to the complex conjugate.
Orthogonality of characters
Consider the 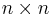 matrix A=A(G) whose matrix elements are
matrix A=A(G) whose matrix elements are 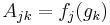 where
where 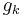 is the kth element of G.
is the kth element of G.
The sum of the entries in the jth row of A is given by
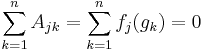 if
if 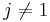 , and
, and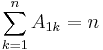 .
.
The sum of the entries in the kth column of A is given by
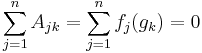 if
if 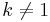 , and
, and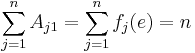 .
.
Let 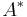 denote the conjugate transpose of A. Then
denote the conjugate transpose of A. Then
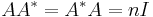 .
.
This implies the desired orthogonality relationship for the characters: i.e.,
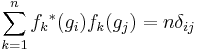 ,
,
where 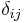 is the Kronecker delta and
is the Kronecker delta and 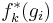 is the complex conjugate of
is the complex conjugate of 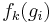 .
.
See also
References
- See chapter 6 of Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR0434929