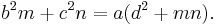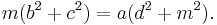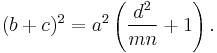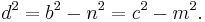Cevian

In geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians. The name cevian comes from the Italian engineer Giovanni Ceva, who proved a well known theorem about cevians which also bears his name.

Length

The length of a cevian can be determined by Stewart's Theorem. In the diagram, the length $d$ can be determined from the formula

$\,b^2m %2B c^2n = a(d^2 %2B mn).$

If the cevian happens to be a median, its length can be determined from the formula

$\,m(b^2 %2B c^2) = a(d^2 %2B m^2).$

If the cevian happens to be an angle bisector, its length can be determined from the formula

$\,(b %2B c)^2 = a^2 \left( \frac{d^2}{mn} %2B 1 \right).$

If the cevian happens to be an altitude, its length can be determined from the formula

$\,d^2 = b^2 - n^2 = c^2 - m^2.$

References

Ross Honsberger (1995) Episodes in Nineteenth and Twentieth Century Euclidean Geometry, pages 13 and 137, Mathematical Association of America.
Vladimir Karapetoff (1929) "Some properties of correlative vertex lines in a plane triangle", American Mathematical Monthly 36:476–9.

Cevian

Length

See also

References