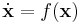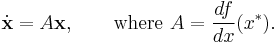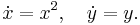Center manifold
In mathematics, the center manifold of an equilibrium point of a dynamical system consists of orbits whose behavior around the equilibrium point is not controlled by either the attraction of the stable manifold or the repulsion of the unstable manifold. The first step when studying equilibrium points of dynamical systems is to linearize the system. The eigenvectors corresponding to eigenvalues with negative real part form the stable eigenspace, which gives rise to the stable manifold. The stable manifold attracts orbits close to it. Similarly, eigenvalues with positive real part yield the unstable manifold, which repels orbits close to it.
This concludes the story if the equilibrium point is hyperbolic (i.e., all eigenvalues of the linearization have nonzero real part). However, if there are eigenvalues whose real part is zero, then these give rise to the center manifold. The behavior near the center manifold is not determined by the linearization and thus more difficult to study.
Center manifolds play an important role in bifurcation theory because the interesting behavior takes place on the center manifold.
Contents |
Definition
Let
be a dynamical system with equilibrium point x*.
The linearization of the system at the equilibrium point is
The matrix A defines three subspaces:
- the stable subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues λ with Re λ < 0;
- the unstable subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues λ with Re λ > 0;
- the center subspace, which is spanned by the generalized eigenvectors corresponding to the eigenvalues λ with Re λ = 0.
These spaces are all invariant subspaces of the linearized equation.
Corresponding to the linearized system, the nonlinear system has invariant manifolds, consisting of orbits of the nonlinear system. There is an invariant manifold tangent to the stable subspace and with the same dimension; this manifold is the stable manifold. Similarly, the unstable manifold is tangent to the unstable subspace, and the center manifold is tangent to the center subspace.[1] If, as is common, the eigenvalues of the center subspace are all precisely zero, rather than just real part zero, then a center manifold is often called a slow manifold.
The center manifold theorem
The center manifold theorem states that if ƒ is Cr (r times continuously differentiable), then at every equilibrium point there is a unique Cr stable manifold, a unique Cr unstable manifold, and a (not necessarily unique) Cr−1 center manifold.[2]
In example applications, a nonlinear coordinate transform to a normal form (mathematics) can clearly separate these three manifolds[3]. A web service [1] currently undertakes the necessary computer algebra for a range of finite dimensional systems.
There is theory for the existence and relevance of center manifolds in infinite dimensional dynamical systems [4]. The general theory currently only applies when the center manifold itself is of finite dimension. However, some applications, such as to shear dispersion, can justify and construct an infinite dimensional center manifold.[5]
Center manifold and the analysis of nonlinear systems
As the stability of the equilibrium correlates with the "stability" of its manifolds, the existence of a center manifold brings up the question about the dynamics on the center manifold. This is analyzed by the center manifold reduction, which, in combination with some system-parameter μ, leads to the concepts of bifurcations.
Correspondingly, a web service [2] currently undertakes the necessary computer algebra to construct just the center manifold for a range of finite dimensional systems.
A simple example
Consider the system
The unstable manifold at the origin is the y axis, and the stable manifold is the trivial set {(0, 0)}. Any orbit not on the stable manifold satisfies an equation on the form 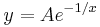 for some real constant A. It follows that for any real A, we can create a center manifold by piecing together the curve
for some real constant A. It follows that for any real A, we can create a center manifold by piecing together the curve 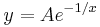 for x > 0 with the negative x axis (including the origin). Moreover, all center manifolds have this potential non-uniqueness, although often the non-uniqueness only occurs in unphysical complex values of the variables.
for x > 0 with the negative x axis (including the origin). Moreover, all center manifolds have this potential non-uniqueness, although often the non-uniqueness only occurs in unphysical complex values of the variables.
The wikipedia entry on slow manifolds gives more examples.
Notes
- ^ Guckenheimer & Holmes (1997), Section 3.2
- ^ Guckenheimer & Holmes (1997), Theorem 3.2.1
- ^ Murdock, James (2003), Normal forms and unfoldings for local dynamical systems, Springer-Verlag
- ^ Mariana Haragus and Gerard Iooss (2011), Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems, Springer
- ^ A.J. Roberts (1988). "The application of centre manifold theory to the evolution of systems which vary slowly in space". J. Austral. Math. Soc. B 29: 480–500. doi:10.1017/S0334270000005968.
References
- Guckenheimer, John; Holmes, Philip (1997), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences, 42, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90819-9, corrected fifth printing.
External links
- Center manifold at Scholarpedia, curated by Jack Carr.