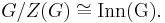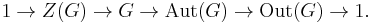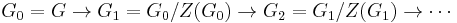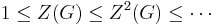Center (group theory)

In abstract algebra, the center of a group G, denoted Z(G),^{[note 1]} is the set of elements that commute with every element of G. In set-builder notation,

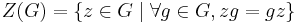$Z(G) = \{z \in G \mid \forall g\in G, zg = gz \}$ .

The center is a subgroup of G, which by definition is abelian (that is commutative). As a subgroup, it is always normal, and indeed characteristic, but it need not be fully characteristic. The quotient group G / Z(G) is isomorphic to the group of inner automorphisms of G.

A group G is abelian if and only if Z(G) = G. At the other extreme, a group is said to be centerless if Z(G) is trivial, i.e. consists only of the identity element.

The elements of the center are sometimes called central.

1 As a subgroup
2 Conjugation
3 Examples
4 Higher centers
- 4.1 Examples
5 Notes
6 See also

As a subgroup

The center of G is always a subgroup of G. In particular:

Z(G) contains e, the identity element of G, because eg = g = ge for all g ∈ G by definition of e, so by definition of Z(G), e ∈ Z(G);
If x and y are in Z(G), then (xy)g = x(yg) = x(gy) = (xg)y = (gx)y = g(xy) for each g ∈ G, and so xy is in Z(G) as well (i.e., Z(G) exhibits closure);
If x is in Z(G), then gx = xg, and multiplying twice, once on the left and once on the right, by x⁻¹, gives x⁻¹g = gx⁻¹ — so x⁻¹ ∈ Z(G).

Furthermore the center of G is always a normal subgroup of G, as it is closed under conjugation.

Conjugation

Consider the map f: G → Aut(G) from G to the automorphism group of G defined by f(g) = φ_g, where φ_g is the automorphism of G defined by

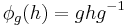$\phi_g(h) = ghg^{-1} \,$ .

This is a group homomorphism, and its kernel is precisely the center of G, and its image is called the inner automorphism group of G, denoted Inn(G). By the first isomorphism theorem we get

$G/Z(G)\cong \rm{Inn}(G).$

The cokernel of this map is the group 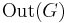$\operatorname{Out}(G)$ of outer automorphisms, and these form the exact sequence

$1 \to Z(G) \to G \to \operatorname{Aut}(G) \to \operatorname{Out}(G) \to 1.$

Examples

The center of an abelian group G is all of G.
The center of a nonabelian simple group is trivial.
The center of the dihedral group D_n is trivial when n is odd. When n is even, the center consists of the identity element together with the 180° rotation of the polygon.
The center of the quaternion group 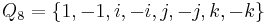$Q_8 = \{1, -1, i, -i, j, -j, k, -k\}$ is $\{1, -1\}$ .
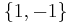The center of the symmetric group S_n is trivial for n ≥ 3.
The center of the alternating group A_n is trivial for n ≥ 4.
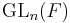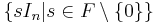The center of the general linear group $\mbox{GL}_n(F)$ is the collection of scalar matrices $\{ sI_n | s \in F\setminus\{0\} \}$ .
The center of the orthogonal group 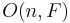$O(n, F)$ is $\{ I_n,-I_n \}$ .
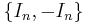The center of the multiplicative group of non-zero quaternions is the multiplicative group of non-zero real numbers.
Using the class equation one can prove that the center of any non-trivial finite p-group is non-trivial.
If the quotient group 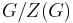$G/Z(G)$ is cyclic, G is abelian (and so G = Z(G), and 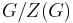$G/Z(G)$ is trivial).
The quotient group 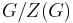$G/Z(G)$ is not isomorphic to the quaternion group $Q_8$ .

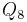Higher centers

Quotienting out by the center of a group yields a sequence of groups called the upper central series:

$G_0 = G \to G_1 = G_0/Z(G_0) \to G_2 = G_1/Z(G_1) \to \cdots$

The kernel of the map 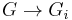$G \to G_i$ is the ith center of G (second center, third center, etc.), and is denoted 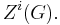$Z^i(G).$ Concretely, the 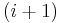$(i%2B1)$ -st center are the terms that commute with all elements up to an element of the ith center. Following this definition, one can define the 0th center of a group to be the identity subgroup. This can be continued to transfinite ordinals by transfinite induction; the union of all the higher centers is called the hypercenter.^{[note 2]}

The ascending chain of subgroups

$1 \leq Z(G) \leq Z^2(G) \leq \cdots$

stabilizes at i (equivalently, 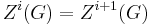$Z^i(G) = Z^{i%2B1}(G)$ ) if and only if 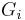$G_i$ is centerless.

Examples

For a centerless group, all higher centers are zero, which is the case 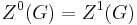$Z^0(G)=Z^1(G)$ of stabilization.
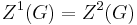By Grün's lemma, the quotient of a perfect group by its center is centerless, hence all higher centers equal the center. This is a case of stabilization at $Z^1(G)=Z^2(G)$ .

Notes

^ The notation Z is from German Zentrum, meaning "center".
^ This union will include transfinite terms if the UCS does not stabilize at a finite stage.

Center (group theory)

Contents

As a subgroup

Conjugation

Examples

Higher centers

Examples

Notes

See also