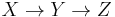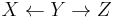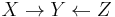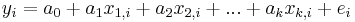Causality

Causality (also referred to as causation^[1]) is the relationship between an event (the cause) and a second event (the effect), where the second event is understood as a consequence of the first.^[2]

In common usage Causality is also the relationship between a set of factors (causes) and a phenomenon (the effect). Anything that affects an effect is a factor of that effect. A direct factor is a factor that affects an effect directly, that is, without any intervening factors. (Intervening factors are sometimes called "intermediate factors.") The connection between a cause(s) and effect in this way can also be referred to as a causal nexus.

Though the causes and effects are typically related to changes or events, candidates include objects, processes, properties, variables, facts, and states of affairs; characterizing the causal relationship can be the subject of much debate.

The philosophical treatment of causality extends over millennia. In the Western philosophical tradition, discussion stretches back at least to Aristotle, and the topic remains a staple in contemporary philosophy.

Contents 1 History 1.1 Western philosophy 1.1.1 Aristotle 1.1.2 After the Middle Ages 1.1.3 Causality, determinism, and existentialism 1.2 Indian philosophy 2 Logic 2.1 Necessary and sufficient causes 2.2 Causality contrasted with conditionals 2.3 Questionable Cause 3 Theories 3.1 Counterfactual theories 3.2 Probabilistic causation 3.3 Causal Calculus 3.4 Structure Learning 3.5 Derivation theories 3.6 Manipulation theories 3.7 Process theories 4 Fields 4.1 Science 4.1.1 Physics 4.1.2 Engineering 4.1.3 Biology and medicine 4.1.4 Psychology 4.1.5 Economics 4.2 Management 4.3 Humanities 4.3.1 History 4.3.2 Law 4.4 Theology 5 See also 6 References 6.1 Other references 7 External links 7.1 Stanford Encyclopedia of Philosophy 7.2 General

History

Western philosophy

Aristotle

Aristotle distinguished between four causes, or four explanations, that each answer the question "why?" in different ways.^[3][4] These various means of explanation can be divided into four general types as follows:

• The material cause is the physical matter, the mass of "raw material" of which something is "made" (of which it consists).
• The formal cause tells us what, by analogy to the plans of an artisan, a thing is intended and planned to be.
• The efficient cause is that external entity from which the change or the ending of the change first starts.
• The final cause is that for the sake of which a thing exists, or is done - including both purposeful and instrumental actions. The final cause, or telos, is the purpose, or end, that something is supposed to serve.

Additionally, things can be causes of one another, reciprocally causing each other, as hard work causes fitness, and vice versa - although not in the same way or by means of the same function: the one is as the beginning of change, the other is as its goal. (Thus Aristotle first suggested a reciprocal or circular causality - as a relation of mutual dependence, action, or influence of cause and effect.) Also; Aristotle indicated that the same thing can be the cause of contrary effects - as its presence and absence may result in different outcomes. In speaking thus he formulated what currently is ordinarily termed a "causal factor," e.g., atmospheric pressure as it affects chemical or physical reactions.

Aristotle marked two modes of causation: proper (prior) causation and accidental (chance) causation. All causes, proper and accidental, can be spoken as potential or as actual, particular or generic. The same language refers to the effects of causes; so that generic effects assigned to generic causes, particular effects to particular causes, and operating causes to actual effects. It is also essential that ontological causality does not suggest the temporal relation of before and after - between the cause and the effect; that spontaneity (in nature) and chance (in the sphere of moral actions) are among the causes of effects belonging to the efficient causation, and that no incidental, spontaneous, or chance cause can be prior to a proper, real, or underlying cause per se.

All investigations of causality coming later in history will consist in imposing a favorite hierarchy on the order (priority) of causes; such as "final > efficient > material > formal" (Thomas Aquinas),^[5] or in restricting all causality to the material and efficient causes or, to the efficient causality (deterministic or chance), or just to regular sequences and correlations of natural phenomena (the natural sciences describing how things happen rather than asking why they happen).

After the Middle Ages

With the end of the Middle Ages however, Aristotle's approach, especially concerning formal and final causes, was criticized by authors such as Niccolò Machiavelli, in the field of political thinking, and Francis Bacon, concerning science more generally. A widely used modern definition of causality was originally given by David Hume.^[5] He denied that we can ever perceive cause and effect, except by developing a habit or custom of mind where we come to associate two types of object or event, always contiguous and occurring one after the other.^[6] In Part III, section XV, Hume expanded this to a list of eight ways of judging whether two things might be cause and effect. The first three:

1. "The cause and effect must be contiguous in space and time."

2. "The cause must be prior to the effect."

3. "There must be a constant union betwixt the cause and effect. 'Tis chiefly this quality, that constitutes the relation."

And then additionally there are three connected criteria which come from our experience and which are "the source of most of our philosophical reasonings":

4. "The same cause always produces the same effect, and the same effect never arises but from the same cause. This principle we derive from experience, and is the source of most of our philosophical reasonings."

5. Hanging upon the above, Hume says that "where several different objects produce the same effect, it must be by means of some quality, which we discover to be common amongst them."

6. And "founded on the same reason": "The difference in the effects of two resembling objects must proceed from that particular, in which they differ."

And then two more:

7. "When any object encreases or diminishes with the encrease or diminution of its cause, 'tis to be regarded as a compounded effect, deriv'd from the union of the several different effects, which arise from the several different parts of the cause."

8. An "object, which exists for any time in its full perfection without any effect, is not the sole cause of that effect, but requires to be assisted by some other principle, which may forward its influence and operation."

However, according to Sowa (2000), citing Max Born in 1949, "relativity and quantum mechanics have forced physicists to abandon these assumptions as exact statements of what happens at the most fundamental levels, but they remain valid at the level of human experience."^[7]

Causality, determinism, and existentialism

The deterministic world-view is one in which the universe is no more than a chain of events following one after another according to the law of cause and effect. To hold this worldview, as an incompatibilist, there is no such thing as "free will". However, compatibilists argue that determinism is compatible with, or even necessary for, free will.

Existentialists have suggested that people believe that while no meaning has been designed in the universe, we each can provide a meaning for ourselves.

Though philosophers have pointed out the difficulties in establishing theories of the validity of causal relations, there is yet the plausible example of causation afforded daily which is our own ability to be the cause of events. This concept of causation does not prevent seeing ourselves as moral agents.

Indian philosophy

Karma is the belief held by some major religions that a person's actions cause certain effects in the current life and/or in future life, positively or negatively. The various philosophical schools (darsanas) provide different accounts of the subject. The doctrine of satkaryavada affirms that the effect inheres in the cause in some way. The effect is thus either a real or apparent modification of the cause. The doctrine of asatkaryavada affirms that the effect does not inhere in the cause, but is a new arising. See Nyaya for some details of the theory of causation in the Nyaya school.

Logic

Necessary and sufficient causes

A similar concept occurs in logic, for this see Necessary and sufficient conditions

Causes are often distinguished into two types: Necessary and sufficient.^[8] A third type of causation, which requires neither necessity nor sufficiency in and of itself, but which contributes to the effect, is called a "contributory cause."^[9]

Necessary causes:

If x is a necessary cause of y, then the presence of y necessarily implies the presence of x. The presence of x, however, does not imply that y will occur.

Sufficient causes:

If x is a sufficient cause of y, then the presence of x necessarily implies the presence of y. However, another cause z may alternatively cause y. Thus the presence of y does not imply the presence of x.

Contributory causes:

A cause may be classified as a "contributory cause," if the presumed cause precedes the effect, and altering the cause alters the effect. It does not require that all those subjects which possess the contributory cause experience the effect. It does not require that all those subjects which are free of the contributory cause be free of the effect. In other words, a contributory cause may be neither necessary nor sufficient but it must be contributory.^[10][11]

J. L. Mackie argues that usual talk of "cause," in fact refers to INUS conditions (insufficient but non-redundant parts of a condition which is itself unnecessary but sufficient for the occurrence of the effect).^[12] For example, a short circuit as a cause for a house burning down. Consider the collection of events: the short circuit, the proximity of flammable material, and the absence of firefighters. Together these are unnecessary but sufficient to the house's burning down (since many other collections of events certainly could have led to the house burning down, for example shooting the house with a flamethrower in the presence of oxygen etc. etc.). Within this collection, the short circuit is an insufficient (since the short circuit by itself would not have caused the fire, but the fire would not have happened without it, everything else being equal) but non-redundant part of a condition which is itself unnecessary (since something else could have also caused the house to burn down) but sufficient for the occurrence of the effect . So, the short circuit is an INUS condition for the occurrence of the house burning down.

Causality contrasted with conditionals

Conditional statements are not statements of causality. An important distinction is that statements of causality require the antecedent to precede or coincide with the consequent in time, whereas conditional statements do not require this temporal order. Confusion commonly arises since many different statements in English may be presented using "If ..., then ..." form (and, arguably, because this form is far more commonly used to make a statement of causality). The two types of statements are distinct, however.

For example, all of the following statements are true when interpreting "If ..., then ..." as the material conditional:

1. If Barack Obama is president of the United States in 2011, then Germany is in Europe.
2. If George Washington is president of the United States in 2011, then <arbitrary statement>.

The first is true since both the antecedent and the consequent are true. The second is true in sentential logic and indeterminate in natural language, regardless of the consequent statement that follows, because the antecedent is false.

The ordinary indicative conditional has somewhat more structure than the material conditional. For instance, although the first is the closest, neither of the preceding two statements seems true as an ordinary indicative reading. But the sentence

• If Shakespeare of Stratford-on-Avon did not write Macbeth, then someone else did.

intuitively seems to be true, even though there is no straightforward causal relation in this hypothetical situation between Shakespeare's not writing Macbeth and someone else's actually writing it.

Another sort of conditional, the counterfactual conditional, has a stronger connection with causality, yet even counterfactual statements are not all examples of causality. Consider the following two statements:

1. If A were a triangle, then A would have three sides.
2. If switch S were thrown, then bulb B would light.

In the first case, it would not be correct to say that A's being a triangle caused it to have three sides, since the relationship between triangularity and three-sidedness is that of definition. The property of having three sides actually determines A's state as a triangle. Nonetheless, even when interpreted counterfactually, the first statement is true.

A full grasp of the concept of conditionals is important to understanding the literature on causality. A crucial stumbling block is that conditionals in everyday English are usually loosely used to describe a general situation. For example, "If I drop my coffee, then my shoe gets wet" relates an infinite number of possible events. It is shorthand for "For any fact that would count as 'dropping my coffee', some fact that counts as 'my shoe gets wet' will be true". This general statement will be strictly false if there is any circumstance where I drop my coffee and my shoe doesn't get wet. However, an "If..., then..." statement in logic typically relates two specific events or facts—a specific coffee-dropping did or did not occur, and a specific shoe-wetting did or did not follow. Thus, with explicit events in mind, if I drop my coffee and wet my shoe, then it is true that "If I dropped my coffee, then I wet my shoe", regardless of the fact that yesterday I dropped a coffee in the trash for the opposite effect—the conditional relates to specific facts. More counterintuitively, if I didn't drop my coffee at all, then it is also true that "If I drop my coffee then I wet my shoe", or "Dropping my coffee implies I wet my shoe", regardless of whether I wet my shoe or not by any means. This usage would not be counterintuitive if it were not for the everyday usage. Briefly, "If X then Y" is equivalent to the first-order logic statement "A implies B" or "not A-and-not-B", where A and B are predicates, but the more familiar usage of an "if A then B" statement would need to be written symbolically using a higher order logic using quantifiers ("for all" and "there exists").

Questionable Cause

Fallacies of questionable cause, also known as causal fallacies, non causa pro causa ("non-cause for cause" in Latin) or false cause, are informal fallacies where a cause is incorrectly identified.

Theories

Counterfactual theories

A counterfactual conditional, subjunctive conditional, or remote conditional, abbreviated cf, is a conditional (or "if-then") statement indicating what would be the case if its antecedent were true. This is to be contrasted with an indicative conditional, which indicates what is (in fact) the case if its antecedent is (in fact) true.

Psychological research shows that people's thoughts about the causal relationships between events influences their judgments of the plausibility of counterfactual alternatives, and conversely, their counterfactual thinking about how a situation could have turned out differently changes their judgements of the causal role of events and agents. Nonetheless, their identification of the cause of an event, and their counterfactual thought about how the event could have turned out differently do not always coincide.^[13] People distinguish between various sorts of causes, e.g., strong and weak causes.^[14] Research in the psychology of reasoning shows that people make different sorts of inferences from different sorts of causes.

Probabilistic causation

Interpreting causation as a deterministic relation means that if A causes B, then A must always be followed by B. In this sense, war does not cause deaths, nor does smoking cause cancer. As a result, many turn to a notion of probabilistic causation. Informally, A probabilistically causes B if A's occurrence increases the probability of B. This is sometimes interpreted to reflect imperfect knowledge of a deterministic system but other times interpreted to mean that the causal system under study is inherently probabilistic, such as quantum mechanics.

Causal Calculus

When experiments are infeasible or illegal, the derivation of cause effect relationship from observational studies must rest on some qualitative theoretical assumptions, for example, that symptoms do not cause diseases, usually expressed in the form of missing arrows in causal graphs such as Bayesian Networks or path diagrams. The mathematical theory underlying these derivations relies on the distinction between conditional probabilities, as in 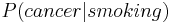, and interventional probabilities, as in 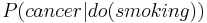. The former reads: "the probability of finding cancer in a person known to smoke" while the latter reads: "the probability of finding cancer in a person forced to smoke". The former is a statistical notion that can be estimated directly in observational studies, while the latter is a causal notion (also called "causal effect") which is what we estimate in a controlled randomized experiment.

The theory of "causal calculus"^[15] permits one to infer interventional probabilities from conditional probabilities in causal Bayesian Networks with unmeasured variables. One very practical result of this theory is the characterization of confounding variables, namely, a sufficient set of variables that, if adjusted for, would yield the correct causal effect between variables of interest. It can be shown that a sufficient set for estimating the causal effect of on is any set of non-descendants of that -separate from after removing all arrows emanating from . This criterion, called "backdoor", provides a mathematical definition of "confounding" and helps researchers identify accessible sets of variables worthy of measurement.

Structure Learning

While derivations in Causal Calculus rely on the structure of the causal graph, parts of the causal structure can, under certain assumptions, be learned from statistical data. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl (1987)^[16] and rests on the distinction between the three possible types of causal substructures allowed in a directed acyclic graph (DAG):

1. 
2. 
3. 

Type 1 and type 2 represent the same statistical dependencies (i.e., and 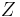are independent given ) and are, therefore, indistinguishable. Type 3, however, can be uniquely identified, since and 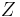are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when and 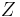have common ancestors, except that one must first condition on those ancestors. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independencies observed.^{[15][17][18][19]}

Alternative methods of structure learning search through the many possible causal structures among the variables, and remove ones which are strongly incompatible with the observed correlations. In general this leaves a set of possible causal relations, which should then be tested by designing appropriate experiments. If experimental data is already available, the algorithms can take advantage of that as well. In contrast with Bayesian Networks, path analysis and its generalization, structural equation modeling, serve better to estimate a known causal effect or test a causal model than to generate causal hypotheses.

For nonexperimental data, causal direction can be hinted if information about time is available. This is because (according to many, though not all, theories) causes must precede their effects temporally. This can be set up by simple linear regression models, for instance, with an analysis of covariance in which baseline and follow up values are known for a theorized cause and effect. The addition of time as a variable, though not proving causality, is a big help in supporting a pre-existing theory of causal direction. For instance, our degree of confidence in the direction and nature of causality is much greater when supported by data from a longitudinal study than by data from a cross-sectional study.

Derivation theories

The Nobel Prize holder Herbert Simon and Philosopher Nicholas Rescher^[20] claim that the asymmetry of the causal relation is unrelated to the asymmetry of any mode of implication that contraposes. Rather, a causal relation is not a relation between values of variables, but a function of one variable (the cause) on to another (the effect). So, given a system of equations, and a set of variables appearing in these equations, we can introduce an asymmetric relation among individual equations and variables that corresponds perfectly to our commonsense notion of a causal ordering. The system of equations must have certain properties, most importantly, if some values are chosen arbitrarily, the remaining values will be determined uniquely through a path of serial discovery that is perfectly causal. They postulate the inherent serialization of such a system of equations may correctly capture causation in all empirical fields, including physics and economics.

Manipulation theories

Some theorists have equated causality with manipulability.^{[21][22][23][24]} Under these theories, x causes y only in the case that one can change x in order to change y. This coincides with commonsense notions of causations, since often we ask causal questions in order to change some feature of the world. For instance, we are interested in knowing the causes of crime so that we might find ways of reducing it.

These theories have been criticized on two primary grounds. First, theorists complain that these accounts are circular. Attempting to reduce causal claims to manipulation requires that manipulation is more basic than causal interaction. But describing manipulations in non-causal terms has provided a substantial difficulty.

The second criticism centers around concerns of anthropocentrism. It seems to many people that causality is some existing relationship in the world that we can harness for our desires. If causality is identified with our manipulation, then this intuition is lost. In this sense, it makes humans overly central to interactions in the world.

Some attempts to save manipulability theories are recent accounts that don't claim to reduce causality to manipulation. These accounts use manipulation as a sign or feature in causation without claiming that manipulation is more fundamental than causation.^[15][25]

Process theories

Some theorists are interested in distinguishing between causal processes and non-causal processes (Russell 1948; Salmon 1984).^[26][27] These theorists often want to distinguish between a process and a pseudo-process. As an example, a ball moving through the air (a process) is contrasted with the motion of a shadow (a pseudo-process). The former is causal in nature while the latter is not.

Salmon (1984)^[26] claims that causal processes can be identified by their ability to transmit an alteration over space and time. An alteration of the ball (a mark by a pen, perhaps) is carried with it as the ball goes through the air. On the other hand an alteration of the shadow (insofar as it is possible) will not be transmitted by the shadow as it moves along.

These theorists claim that the important concept for understanding causality is not causal relationships or causal interactions, but rather identifying causal processes. The former notions can then be defined in terms of causal processes.

Fields

Science

Causality is a basic assumption of science. Within the scientific method, scientists set up experiments to determine causality in the physical world. Embedded within the scientific method and experiments is a hypothesis or several hypotheses about causal relationships. The scientific method is used to test the hypotheses.

Physics

Physicists conclude that certain elemental forces (gravity, the strong and weak nuclear forces, and electromagnetism) are the four fundamental forces that cause all other events in the universe. The notion of causality that appears in many different physical theories is hard to interpret in ordinary language. One problem is typified by earth's interaction with the moon. It is inaccurate to say, "the moon exerts a gravitic pull and then the tides rise." In Newtonian mechanics gravity, rather, is a constant observable relationship among masses, and the movement of the tides is an example of that relationship. There are no discrete events or "pulls" that can be said to precede the rising of tides. Interpreting gravity causally is even more complicated in general relativity. Similarly, quantum mechanics is another branch of physics in which the concept of causality is challenged by paradoxes. For statistical generalization, causality has further implications due to its intimate connection with the Second Law of Thermodynamics (see the fluctuation theorem).

Engineering

A causal system is a system with output and internal states that depends only on the current and previous input values. A system that has some dependence on input values from the future (in addition to possible past or current input values) is termed an acausal system, and a system that depends solely on future input values is an anticausal system. Acausal filters, for example, can only exist as postprocessing filters, because these filters can extract future values from a memory buffer or a file.

Biology and medicine

Austin Bradford Hill built upon the work of Hume and Popper and suggested in his paper "The Environment and Disease: Association or Causation?" that aspects of an association such as strength, consistency, specificity and temporality be considered in attempting to distinguish causal from noncausal associations in the epidemiological situation. See Bradford-Hill criteria.

Psychology

Psychologists take an empirical approach to causality, investigating how people and non-human animals detect or infer causation from sensory information, prior experience and innate knowledge.

Attribution

Attribution theory is the theory concerning how people explain individual occurrences of causation. Attribution can be external (assigning causality to an outside agent or force - claiming that some outside thing motivated the event) or internal (assigning causality to factors within the person - taking personal responsibility or accountability for one's actions and claiming that the person was directly responsible for the event). Taking causation one step further, the type of attribution a person provides influences their future behavior.

The intention behind the cause or the effect can be covered by the subject of action (philosophy). See also accident; blame; intent; and responsibility.

Causal powers

Whereas David Hume argued that causes are inferred from non-causal observations, Immanuel Kant claimed that people have innate assumptions about causes. Within psychology, Patricia Cheng (1997)^[28] attempted to reconcile the Humean and Kantian views. According to her power PC theory, people filter observations of events through a basic belief that causes have the power to generate (or prevent) their effects, thereby inferring specific cause-effect relations. The theory assumes probabilistic causation. Pearl (2000)^[15] has shown that Cheng's causal power can be given a counterfactual interpretation, (i.e., the probability that, absent and , would be true if were true) and is computable therefore using structural models. Within a Bayesian framework, the power PC theory can be interpreted as a noisy-OR function used to compute likelihoods (Griffiths & Tenenbaum, 2005)^[29]

Causation and salience

Our view of causation depends on what we consider to be the relevant events. Another way to view the statement, "Lightning causes thunder" is to see both lightning and thunder as two perceptions of the same event, viz., an electric discharge that we perceive first visually and then aurally.

Naming and causality

While the names we give objects often refer to their appearance, they can also refer to an object's causal powers - what that object can do, the effects it has on other objects or people. David Sobel and Alison Gopnik from the Psychology Department of UC Berkeley designed a device known as the blicket detector, which suggests that "when causal property and perceptual features are equally evident, children are equally as likely to use causal powers as they are to use perceptual properties when naming objects".

Perception of Launching Events

Some researchers such as Anjan Chatterjee at the University of Pennsylvania and Jonathan Fugelsang at the University of Waterloo are using neuroscience techniques to investigate the neural and psychological underpinnings of causal launching events in which one object causes another object to move. Both temporal and spatial factors can be manipulated.

Economics

Economics usually employs pre-existing data rather than experimental data to infer causality. The body of statistical techniques that are used in economics is referred to as econometrics, and involves substantial use of regression analysis. Typically a linear relationship such as

is postulated, in which 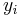is the i^th observation of the dependent variable (hypothesized to be the caused variable), 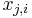for j=1,...,k is the i^th observation on the j^th independent variable (hypothesized to be a causative variable), and 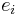is the error term for the i^th observation (containing the combined effects of all other causative variables, which must be uncorrelated with the included independent variables). If there is reason to believe that none of the 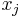s is caused by y, then estimates of the coefficients 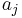are obtained. If the null hypothesis that 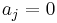is rejected, then the alternative hypothesis that 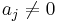and equivalently that 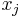causes y cannot be rejected. On the other hand, if the null hypothesis that 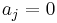cannot be rejected, then equivalently the hypothesis of no causal effect of 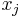on y cannot be rejected. Here the notion of causality is one of contributory causality as discussed above: If the true value 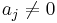, then a change in 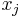will result in a change in y unless some other causative variable(s), either included in the regression or implicit in the error term, change in such a way as to exactly offset its effect; thus a change in 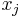is not sufficient to change y. Likewise, a change in 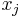is not necessary to change y, because a change in y could be caused by something implicit in the error term (or by some other causative explanatory variable included in the model).

The above way of testing for causality requires belief that there is no reverse causation, in which y would cause 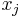. This belief can be established in one of several ways. First, the variable 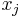may be a non-economic variable: for example, if rainfall amount 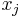is hypothesized to affect the futures price y of some agricultural commodity, it is impossible that in fact the futures price affects rainfall amount (provided that cloud seeding is never attempted). Second, the instrumental variables technique may be employed to remove any reverse causation by introducing a role for other variables (instruments) that are known to be unaffected by the dependent variable. Third, the principle that effects cannot precede causes can be invoked, by including on the right side of the regression only variables that precede in time the dependent variable; this principle is invoked, for example, in testing for Granger causality and in its multivariate analog, vector autoregression, both of which control for lagged values of the dependent variable while testing for causal effects of lagged independent variables.

Regression analysis controls for other relevant variables by including them as regressors (explanatory variables). This helps to avoid false inferences of causality due to the presence of a third, underlying, variable that influences both the potentially causative variable and the potentially caused variable: its affect on the potentially caused variable is captured by directly including it in the regression, so that effect will not be picked up as an indirect effect through the potentially causative variable of interest.

Management

For quality control in manufacturing in the 1960s, Kaoru Ishikawa developed a cause and effect diagram, known as an Ishikawa diagram or fishbone diagram. The diagram categorizes causes, such as into the six main categories shown here. These categories are then sub-divided. Ishikawa's method identifies "causes" in brainstorming sessions conducted among various groups involved in the manufacturing process. These groups can then be labeled as categories in the diagrams. The use of these diagrams has now spread beyond quality control, and they are used in other areas of management and in design and engineering. Ishikawa diagrams have been criticized for failing to make the distinction between necessary conditions and sufficient conditions. It seems that Ishikawa was not even aware of this distinction.^[30]

Humanities

History

In the discussion of history, events are often considered as if in some way being agents that can then bring about other historical events. Thus, the combination of poor harvests, the hardships of the peasants, high taxes, lack of representation of the people, and kingly ineptitude are among the causes of the French Revolution. This is a somewhat Platonic and Hegelian view that reifies causes as ontological entities. In Aristotelian terminology, this use approximates to the case of the efficient cause.

Law

According to law and jurisprudence, legal cause must be demonstrated to hold a defendant liable for a crime or a tort (i.e. a civil wrong such as negligence or trespass). It must be proven that causality, or a "sufficient causal link" relates the defendant's actions to the criminal event or damage in question. Causation is also an essential legal element that must be proven to qualify for remedy measures under international trade law.^[31]

Theology

Note the concept of omnicausality in theology and in philosophy.^[32]

See also

Statistics: Causal loop diagram Causal Markov condition Correlation does not imply causation Experimental design Granger causality Linear regression Randomness Rubin Causal Model Validity (statistics) Physics: Anthropic principle Arrow of time Butterfly effect Chain reaction Grandfather paradox Quantum Zeno effect Retrocausality Schrödinger's cat Wheeler-Feynman absorber theory

Philosophy: Aetiology Chance (philosophy) Chicken or the egg Condition of possibility Determinism Mill's Methods Newcomb's paradox Ontological paradox Post hoc ergo propter hoc Predestination paradox Proximate and ultimate causation Non sequitur (logic) General Cosmological argument Domino effect Sequence of events Mathematics: Causal filter Causal system Causality conditions Chaos theory

Psychology & Medicine: Adverse effect Clinical trial Force Dynamics Iatrogenesis Nocebo Placebo Scientific control Synchronicity Suggestibility Suggestion Sociology & Economics: Instrumental variable Root cause analysis Self-fulfilling prophecy Unintended consequence Virtuous circle and vicious circle

References

Other references

• Spirtes, Peter, Clark Glymour and Richard Scheines Causation, Prediction, and Search, MIT Press, ISBN 0-262-19440-6
• University of California journal articles, including Judea Pearl's articles between 1984-1998 [2].
• Schimbera, Jürgen / Schimbera, Peter: Determination des Indeterminierten. Kritische Anmerkungen zur Determinismus- und Freiheitskontroverse. Verlag Dr. Kovac, Hamburg 2010, ISBN 978-3-8300-5099-5. 

External links

• "The Art and Science of Cause and Effect": a slide show and tutorial lecture by Judea Pearl
• Donald Davidson: Causal Explanation of Action The Internet Encyclopedia of Philosophy
• leadsto: a public available collection comprising more than 5000 causalities
• Causal inference in statistics: An overview, by Judea Pearl (September 2009)

Stanford Encyclopedia of Philosophy

• Backwards Causation
• Causal Processes
• Causation and Manipulability
• Causation in the Law
• Counterfactual Theories of Causation
• Medieval Theories of Causation
• Probabilistic Causation
• The Metaphysics of Causation

General

• Dictionary of the History of Ideas: Causation
• Dictionary of the History of Ideas: Causation in History
• Dictionary of the History of Ideas: Causation in Law
• People's Epidemiology Library

Links to related articles Time Major concepts Time · Eternity · Arguments for eternity · Immortality Deep time · History · Past · Present · Future · Future studies Time Portal Measurement and standards Chronometry · UTC · UT · TAI · Second · Minute · Hour · Sidereal time · Solar time · Time zone Clock · Astrarium · History of timekeeping devices · Horology · Marine chronometer · Sundial · Water clock Calendar · Day · Week · Month · Year · Tropical year · Gregorian · Islamic · Julian Intercalation · Leap second · Leap year Chronology Astronomical chronology · Calendar era · Chronicle · Dating methodologies · Geochronology Geologic Time · Geological history · Periodization · Regnal year · Timeline Religion and mythology Dreamtime · Kāla · Kalachakra · Prophecy · Time and fate deities · Wheel of time Philosophy A-series and B-series · B-Theory of time · Causality · Endurantism · Eternal return · Eternalism · Event Perdurantism · Presentism · Temporal finitism · Temporal parts · The Unreality of Time Physical sciences Time in physics · Absolute time and space · Arrow of time · Chronon · Coordinate time Planck epoch · Planck time · Proper time · Spacetime · Theory of relativity Time dilation · Gravitational time dilation · Time domain · T-symmetry Biology Chronobiology · Circadian rhythms Psychology Mental chronometry · Sense of time · Specious present Sociology and anthropology Long Now Foundation · Time discipline · Time use research Economics Time value of money · Time-based currency · Time Banking Related topics Carpe diem · Duration · Hexadecimal time · Metric time · Space · System time · Tempus fugit Time capsule · Time signature · Time travel Philosophy of time Concepts in time Time · Duration · A priori and a posteriori · Eternity · Event  · Action · Deterministic system · Free will · Eternal return · A-series and B-series · Temporal parts · Growing block universe Time Portal Theories of time Determinism · Temporal finitism · Fatalism · Indeterminism · Compatibilism and incompatibilism · Presentism · Eternalism · Four dimensionalism · Endurantism · Perdurantism  · B-Theory of time Related articles Metaphysics · Etiology · Teleology · Post hoc ergo propter hoc · The Unreality of Time Philosophy Branches Metaphysics · Epistemology · Logic · Ethics · Aesthetics Philosophy of Action · Art · Being · Biology · Chemistry · Computer science · Education · Economics · Engineering · Environment · Film · Geography · Information · Healthcare · History · Human nature · Humor · Language · Law · Literature · Mathematics · Mind · Music · Pain · Philosophy · Physics · Politics · Psychology · Religion (Hermeneutics) · Science · Sexuality · Social science · Technology · War Schools of thought By historical era Ancient  · Western (Medieval · Renaissance · Modern · Contemporary) Ancient Chinese (Agriculturalism · Confucianism · Legalism · Logicians · Mohism · Chinese naturalism · Neotaoism · Taoism · Zen) · Greek & Greco-Roman (Aristotelianism · Cynicism · Epicureanism · Neoplatonism · Peripatetic · Platonism · Presocratic · Pythagoreanism · Sophism · Stoicism) · Indian (Buddhist · Cārvāka · Hindu · Jain) · Persian (Mazdakism · Zoroastrianism · Zurvanism) 9th–16th centuries Christian Europe (Scholasticism · Renaissance humanism · Thomism) · East Asian (Korean Confucianism · Rigaku · Neo-Confucianism) · Islamic (Averroism · Avicennism · Persian Illuminationism · Kalam · Sufi) · Jewish (Judeo-Islamic) 17th–21st centuries Absolute idealism · Australian realism · Behaviorism · Cartesianism · Classical liberalism · Deconstruction · Dialectical materialism · Epiphenomenalism · Egoism · Existentialism · Feminist · Functionalism · Hegelianism · Kantianism · Kyoto school · Legal positivism · Logical positivism · Marxism · Mitogaku · Modernism · Neo-Kantianism · New Confucianism · New Philosophers · Objectivism · Ordinary language · Particularism · Phenomenology · Postmodernism · Post-structuralism · Pragmatism · Reformed epistemology · Structuralism · Transcendentalism · Utilitarianism · more... Positions Certainty (Skepticism · Solipsism · Nihilism) · Ethics (Consequentalism · Deontology · Virtue) · Free will (Compatibilism · Determinism · Libertarianism) · Metaphysics (Atomism · Dualism · Monism · Naturalism) · Epistemology (Constructivism · Empiricism · Idealism · Rationalism) · Naturalism · Normativity (Absolutism · Particularism · Relativism · Universalism) · Ontology (Action · Event · Process) · Reality (Anti-realism · Idealism · Materialism · Realism) By region African · American · Greek · Aztec · British · Chinese · Danish · French · German · Indian · Indonesian · Iranian · Italian · Japanese · Korean · Polish · Romanian Lists Outline · Index · Schools · Glossary · Philosophers · Movements · Publications Portal · Category · WikiProject · changes Metaphysics Metaphysicians Parmenides · Plato · Aristotle · Kapila · Plotinus · Duns Scotus · Thomas Aquinas · René Descartes · John Locke · David Hume · Immanuel Kant · Isaac Newton · Arthur Schopenhauer · Baruch Spinoza · Georg W. F. Hegel · George Berkeley · Gottfried Leibniz · Henri Bergson · Friedrich Nietzsche · Charles Sanders Peirce · Ludwig Wittgenstein · Martin Heidegger · Alfred N. Whitehead · Bertrand Russell · Dorothy Emmet · G. E. Moore · Jean-Paul Sartre · Gilbert Ryle · Hilary Putnam · P. F. Strawson · R. G. Collingwood · Adolph Stöhr · Rudolf Carnap · Saul Kripke · Willard V. O. Quine · Donald Davidson · more ... Theories Anti-realism · Cartesian dualism · Free will · Liberty · Materialism · Meaning of life · Idealism · Existentialism · Essentialism · Libertarianism · Determinism · Naturalism · Monism · Platonic idealism · Hindu idealism · Phenomenalism · Nihilism · Realism · Physicalism · MOQ · Relativism · Scientific realism · Solipsism · Subjectivism · Substance theory · Type theory · Sankhya Concepts Action · Abstract object · Being · Category of being · Causality · Change · Choice · Concept · Cogito ergo sum · Embodied cognition · Entity · Essence · Existence · Experience · Form · Idea · Identity · Information · Insight · Intelligence · Intention · Matter · Memetics · Mind · Meaning · Mental representation · Modality · Motion · Necessity · Notion · Object · Pattern · Physical object · Perception · Principle · Properties · Qualia · Quality · Reality · Subject · Soul · Substance · Thought · Time · Truth · Type · Universal · Unobservable · Value · World soul · more ... Related articles Cosmology · Epistemology · Ontology · Teleology · Philosophy of psychology · Philosophy of mind · Philosophy of self · Philosophy of space and time · Axiology · Theoretical physics · meta- Portal · Category · Task Force · Stubs · Discussion Epistemology Epistemologists Thomas Aquinas · Robert Audi · A. J. Ayer · George Berkeley · Laurence BonJour · René Descartes · Edmund Gettier · Alvin Goldman · Nelson Goodman · Paul Grice · David Hume · Immanuel Kant · Søren Kierkegaard · John Locke · G. E. Moore · Robert Nozick · Alvin Plantinga · Plato · Louis Pojman · P. F. Strawson · W.V.O. Quine · Bertrand Russell · Ludwig Wittgenstein · Vienna Circle Theories Coherentism · Constructivist epistemology · Contextualism · Determinism · Empiricism · Fallibilism · Foundationalism · Holism · Infinitism · Innatism · Internalism and externalism · Naïve realism · Naturalized epistemology · Objectivist epistemology · Phenomenalism · Positivism · Reductionism · Reliabilism · Representative realism · Rationalism · Skepticism · Theory of Forms · Transcendental idealism · Uniformitarianism Concepts Knowledge · Justification · Belief · Perception · A priori knowledge · Induction · Other minds · Analytic-synthetic distinction · Causality · Common sense · Descriptive knowledge · Gettier problem · Objectivity · Analysis · Proposition · Regress argument · Simplicity · Speculative reason · Truth · more... Related articles Outline of epistemology · Alethiology · Formal epistemology · Meta-epistemology · Philosophy of perception · Philosophy of science · Faith and rationality · Social epistemology Portal · Category · Task Force · Stubs · Discussion Philosophy of science Philosophers Albert Einstein · Alfred North Whitehead · Aristotle · Auguste Comte · Averroes · Berlin Circle · Carl Gustav Hempel · C. D. Broad · Charles Sanders Peirce · Dominicus Gundissalinus · Daniel Dennett · Epicurians · Francis Bacon · Friedrich Schelling · Galileo Galilei · Henri Poincaré · Herbert Spencer · Hugh of Saint Victor · Immanuel Kant · Imre Lakatos · Isaac Newton · John Dewey · John Stuart Mill · Jürgen Habermas · Karl Pearson · Karl Popper · Karl Theodor Jaspers · Larry Laudan · Otto Neurath · Paul Haeberlin · Paul Feyerabend · Pierre Duhem · Pierre Gassendi · Plato · R.B. Braithwaite · René Descartes · Robert Kilwardby · Roger Bacon · Rudolf Carnap · Stephen Toulmin · Stoicism · Thomas Hobbes · Thomas Samuel Kuhn · Vienna Circle · W.V.O. Quine · Wilhelm Windelband · Wilhelm Wundt · William of Ockham · William Whewell · more... Concepts Analysis · Analytic-synthetic distinction · A priori and a posteriori · Artificial intelligence · Causality · Commensurability · Construct · Demarcation problem · Explanatory power · Fact · Falsifiability · Ignoramus et ignorabimus · Inductive reasoning · Ingenuity · Inquiry · Models of scientific inquiry · Nature · Objectivity · Observation · Paradigm · Problem of induction · Scientific explanation · Scientific law · Scientific method · Scientific revolution · Scientific theory · Testability · Theory choice · Metatheory of science Confirmation holism · Coherentism · Contextualism · Conventionalism · Deductive-nomological model · Determinism · Empiricism · Fallibilism · Foundationalism · Hypothetico-deductive model · Infinitism · Instrumentalism · Naturalism · Positivism · Pragmatism · Rationalism · Received view of theories · Reductionism · Semantic view of theories · Scientific realism · Scientism · Scientific anti-realism · Skepticism · Uniformitarianism · Vitalism · Metaphysics Related Epistemology · History and philosophy of science · History of science · History of evolutionary thought · Philosophy of biology · Philosophy of chemistry · Philosophy of physics · Philosophy of mind · Philosophy of artificial intelligence · Philosophy of information · Philosophy of perception · Philosophy of space and time · Philosophy of thermal and statistical physics · Philosophy of social sciences · Philosophy of environment · Philosophy of psychology · Philosophy of technology · Philosophy of computer science · Pseudoscience · Relationship between religion and science · Rhetoric of science · Sociology of scientific knowledge · Criticism of science · Alchemy · more... Portal · Category · Task Force · Discussion · Changes