Cauchy's theorem (geometry)
Cauchy's theorem is a theorem in geometry, named after Augustin Cauchy. It states that convex polytopes in three dimensions with congruent corresponding faces must be congruent to each other. That is, any polyhedral net formed by unfolding the faces of the polyhedron onto a flat surface, together with gluing instructions describing which faces should be connected to each other, uniquely determines the shape of the original polyhedron. For instance, if six squares are connected together in the pattern of a cube, then they must form a cube: there is no convex polyhedron with six square faces connected in the same way that does not have the same shape.
This is a foundational result in rigidity theory: one consequence of the theorem is that, if one makes a physical model of a convex polyhedron by connecting together rigid plates for each of the polyhedron faces with flexible hinges along the polyhedron edges, then this ensemble of plates and hinges will necessarily form a rigid structure.
Contents |
Statement
Let P and Q be combinatorially equivalent 3-dimensional convex polytopes; that is, they are convex polytopes with isomorphic face lattices. Suppose further that each pair of corresponding faces from P and Q are congruent to each other, i.e. equal up to a rigid motion. Then P and Q are themselves congruent.
History
The result originated in Euclid's Elements, where solids are called equal if the same holds for their faces. This version of the result was proved by Cauchy in 1813 based on earlier work by Lagrange. A technical mistake was found by Steinitz in 1920's and later corrected by him (1928) and Alexandrov (1950). A definitive modern version of the proof was given by Stoker (1968).
- The result does not hold on a plane or for non-convex polyhedra in
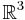 : there exist non-convex flexible polyhedra that have one or more degrees of freedom of movement that preserve the shapes of their faces. In particular, Connelly' sphere, a flexible non-convex polyhedron homeomorphic to a 2-sphere was discovered by Robert Connelly in 1977.
: there exist non-convex flexible polyhedra that have one or more degrees of freedom of movement that preserve the shapes of their faces. In particular, Connelly' sphere, a flexible non-convex polyhedron homeomorphic to a 2-sphere was discovered by Robert Connelly in 1977. - Although originally proven by Cauchy in three dimensions, the theorem was extended to dimensions higher than 3 by Alexandrov (1950).
- Cauchy's rigidity theorem is a corollary from Cauchy's theorem stating that a convex polytope cannot be deformed so that its faces remain rigid.
- In 1974 Herman Gluck showed that in a certain precise sense almost all (non-convex) polyhedra are rigid.
- Dehn's rigidity theorem is an extension of the Cauchy rigidity theorem to infinitesimal rigidity. This result was obtained by Dehn in 1916.
- Pogorelov's uniqueness theorem is a result by Pogorelov generalizing Alexandrov's uniqueness theorem to general convex surfaces.
- Alexandrov's uniqueness theorem is a result by Alexandrov (1950), weakening conditions of the Cauchy theorem to convex polytopes which are intrinsically isometric.
- The analogue uniqueness theorem for smooth surfaces was proved by Cohn-Vossen in 1927.
- Bricard's octahedra are self-intersecting flexible surfaces discovered by a French mathematician Raoul Bricard in 1897.
References
- A.L. Cauchy, "Recherche sur les polyèdres - premier mémoire", Journal de l'Ecole Polytechnique 9 (1813), 66–86.
- M. Dehn, "Über die Starreit konvexer Polyeder" (in German), Math. Ann. 77 (1916), 466-473.
- A.D. Alexandrov, Convex polyhedra, GTI, Moscow, 1950. English translation: Springer, Berlin, 2005.
- J.J. Stoker, "Geometrical problems concerning polyhedra in the large", Comm. Pure Appl. Math. 21 (1968), 119-168.
- R. Connelly, "The Rigidity of Polyhedral Surfaces", Mathematics Magazine 52 (1979), 275-283
- R. Connelly, "Rigidity", in Handbook of Convex Geometry, vol. A, 223-271, North-Holland, Amsterdam, 1993.