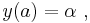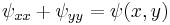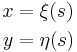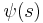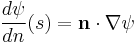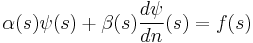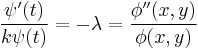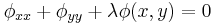Cauchy boundary condition
In mathematics, a Cauchy boundary condition ( /koʊˈʃiː/) imposed on an ordinary differential equation or a partial differential equation specifies both the values a solution of a differential equation is to take on the boundary of the domain and the normal derivative at the boundary. It corresponds to imposing both a Dirichlet and a Neumann boundary condition. It is named after the prolific 19th century French mathematical analyst Augustin Louis Cauchy.
Cauchy boundary conditions can be understood from the theory of second order, ordinary differential equations, where to have a particular solution one has to specify the value of the function and the value of the derivative at a given initial or boundary point, i.e.,
and
where 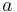 is a boundary or initial point.
is a boundary or initial point.
Cauchy boundary conditions are the generalization of these type of conditions. Let us first recall a simplified form for writing partial derivatives.
and let us now define a simple, second order, partial differential equation:
We have a two dimensional domain whose boundary is a boundary line, which in turn can be described by the following parametric equations
hence, in a similar manner as for second order, ordinary differential equations, we now need to know the value of the function at the boundary, and its normal derivative in order to solve the partial differential equation, that is to say, both
and
are specified at each point on the boundary of the domain of the given partial differential equation (PDE), where  is the gradient of the function. It is sometimes said that Cauchy boundary conditions are a weighted average of imposing Dirichlet boundary conditions and Neumann boundary conditions. This should not be confused with statistical objects such as the weighted mean, the weighted geometric mean or the weighted harmonic mean, since no such formulas are used upon imposing Cauchy boundary conditions. Rather, the term weighted average means that while analyzing a given boundary value problem, one should bear in mind all available information for its well-posedness and subsequent successful solution.
is the gradient of the function. It is sometimes said that Cauchy boundary conditions are a weighted average of imposing Dirichlet boundary conditions and Neumann boundary conditions. This should not be confused with statistical objects such as the weighted mean, the weighted geometric mean or the weighted harmonic mean, since no such formulas are used upon imposing Cauchy boundary conditions. Rather, the term weighted average means that while analyzing a given boundary value problem, one should bear in mind all available information for its well-posedness and subsequent successful solution.
Since the parameter 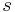 is usually time, Cauchy conditions can also be called initial value conditions or initial value data or simply Cauchy data.
is usually time, Cauchy conditions can also be called initial value conditions or initial value data or simply Cauchy data.
Notice that although Cauchy boundary conditions imply having both Dirichlet and Neumann boundary conditions, this is not the same at all as having Robin or impedance boundary condition, a mixture of Dirichlet and Neumann boundary conditions are given by
where  ,
,  , and
, and 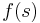 are understood to be given on the boundary (this contrasts to the term mixed boundary conditions, which is generally taken to mean boundary conditions of different types on different subsets of the boundary). In this case the function and its derivative must fulfill a condition within the same equation for the boundary condition.
are understood to be given on the boundary (this contrasts to the term mixed boundary conditions, which is generally taken to mean boundary conditions of different types on different subsets of the boundary). In this case the function and its derivative must fulfill a condition within the same equation for the boundary condition.
Contents |
Example
Let us define the heat equation in two spatial dimensions as follows
where 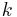 is a material-specific constant called thermal conductivity
is a material-specific constant called thermal conductivity
and suppose that such equation is applied over the region 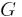 , which is the upper semidisk of radius
, which is the upper semidisk of radius 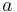 centered at the origin. Suppose that the temperature is held at zero on the curved portion of the boundary, while the straight portion of the boundary is insulated, i.e., we define the Cauchy boundary conditions as
centered at the origin. Suppose that the temperature is held at zero on the curved portion of the boundary, while the straight portion of the boundary is insulated, i.e., we define the Cauchy boundary conditions as
and
We can use separation of variables by considering the function as composed by the product of the spatial and the temporal part
applying such product to the original equation we obtain
whence
Since the left hand side (l.h.s.) depends only on 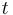 , and the right hand side (r.h.s) depends only on
, and the right hand side (r.h.s) depends only on 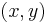 , we conclude that both should be equal to the same constant
, we conclude that both should be equal to the same constant
Thus we are led to two equations: the first in the spatial variables
and a second equation in the 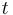 variable,
variable,
Once we impose the boundary conditions, the solution of the temporal ODE is
where A is a constant which could be defined upon the initial conditions. The spatial part can be solved again by separation of variables, substituting 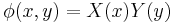 into the PDE and dividing by
into the PDE and dividing by  from which we obtain (after reorganizing terms)
from which we obtain (after reorganizing terms)
since the l.h.s depends only on y and r.h.s only depends on 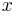 , both sides must equal a constant, say
, both sides must equal a constant, say  ,
,
so we obtain a pair of ODE's upon which we can impose the boundary conditions that we defined
See also
- Dirichlet boundary condition
- Mixed boundary condition
- Neumann boundary condition
- Robin boundary condition
References
- Cooper, Jeffery M. "Introduction to Partial Differential Equations with MATLAB". ISBN 0-8176-3967-5