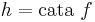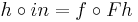Catamorphism
In category theory, the concept of catamorphism (from Greek: κατά = downwards or according to; μορφή = form or shape) denotes the unique homomorphism from an initial algebra into some other algebra. The concept has been applied to functional programming as folds.
The dual concept is that of anamorphism. See also Hylomorphism (computer science)
Contents |
Catamorphisms in functional programming
In functional programming, a catamorphism is a generalization of the folds on lists known from functional programming to arbitrary algebraic data types that can be described as initial algebras.
One of the first publications to introduce the notion of a catamorphism in the context of programming was the paper “Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire”, by Erik Meijer et al.[1], which was in the context of the Squiggol formalism.
The dual concept is that of anamorphisms, a generalization of unfolds.
Example
The following example is in Haskell:
data Tree a = Leaf a | Branch (Tree a) (Tree a) type TreeAlgebra a r = (a -> r, r -> r -> r) foldTree :: TreeAlgebra a r -> Tree a -> r foldTree (f, g) (Leaf x) = f x foldTree (f, g) (Branch l r) = g (foldTree (f, g) l) (foldTree (f, g) r) treeDepth :: TreeAlgebra a Integer treeDepth = (const 1, \l r -> 1 + max l r) sumTree :: (Num a) => TreeAlgebra a a sumTree = (id, (+))
Here foldTree (f, g) is a catamorphism for the Tree a datatype; treeDepth and sumTree are called algebras.
Catamorphisms in category theory
Category theory provides the necessary concepts to give a generic definition that accounts for all initial data types (using an identification of functions in functional programming with the morphisms of the category Set or some related concrete category). This was done by Grant Malcolm[1][2].
Returning to the above example, consider a functor F sending r to a + r × r. An F-algebra for this specific case is a pair (r, [f1,f2]), where r is an object, and two morphisms, f1 and f2 are defined as f1: a → r, and f2: r × r → r.
In the category of F-algebras over such F, an initial algebra, if it exists, represents a Tree, or, in Haskell terms, it is (Tree a, [Leaf, Branch]).
Tree a being an initial object in the category of F-algebras, there is a unique homomorphism of F-algebras from Tree a to any given F-algebra. This unique homomorphism is called catamorphism.
The general case
In category theory, catamorphisms are the categorical dual of anamorphisms (and anamorphisms are the categorical dual of catamorphisms).
That means the following. Suppose (A, in) is an initial F-algebra for some endofunctor F of some category into itself. Thus, in is a morphism from FA to A, and since it is assumed to be initial we know that whenever (X, f) is another F-algebra (a morphism f from FX to X), there will be a unique homomorphism h from (A, in) to (X, f), that is a morphism h from A to X such that h . in = f . Fh. Then for each such f we denote by cata f that uniquely specified morphism h.
In other words, we have the following defining relationship, given some fixed F, A, and in as above:
Notation
Another notation for cata f found in the literature is 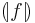 . The open brackets used are known as banana brackets, after which catamorphisms are sometimes referred to as bananas, as mentioned in Meijer 1991.
. The open brackets used are known as banana brackets, after which catamorphisms are sometimes referred to as bananas, as mentioned in Meijer 1991.
See also
References
- Erik Meijer, Maarten Fokkinga, and Ross Paterson. Functional Programming with Bananas, Lenses, Envelopes, and Barbed Wire [2], contains additional definitions and examples
- ^ Malcolm, Grant (1990) (Ph.D. Thesis), Algebraic types and program transformation, University of Groningen.
- ^ Malcolm, Grant (1990), "Data structures and program transformation", Science of Computer Programming 14 (2-3): 255–279, doi:10.1016/0167-6423(90)90023-7.
External links
Detailed example
Brian McNamara, a developer on the F# team, has created a series of blog posts that describe catamorphisms and their synergy with tail recursion, continuations and monads. He explores how the concept of catamorphism interacts with other functional tools.
- Catamorphisms, part one (Initial example)
- Catamorphisms, part two (Generalization for arbitrary data structures, example: processing binary trees, application of tail recursion)
- Catamorphisms, part three (Example: processing an AST)
- Catamorphisms, part four (Using catamorphisms to produce new ASTs)
- Catamorphisms, part five (Minimizing memory pressure for AST rewriting task, application of continuations)
- Catamorphisms, part six (Making code from previous article to be tail-recursive)
- Catamorphisms, part seven (Using monads to reduce boilerplate)