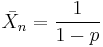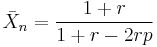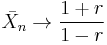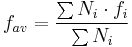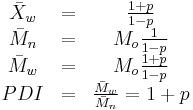Carothers equation
In step-growth polymerization, the Carothers equation (or Carothers' equation) gives the degree of polymerization, Xn, for a given fractional monomer conversion, p.
There are several versions of this equation, proposed by Wallace Carothers who invented nylon in 1935.
Contents |
Linear polymers: two monomers in equimolar quantities
The simplest case refers to the formation of a strictly linear polymer by the reaction (usually by condensation) of two monomers in equimolar quantities. An example is the synthesis of nylon-6,6 whose formula is [-NH-(CH2)6-NH-CO-(CH2)4-CO-]n from one mole of hexamethylenediamine, H2N(CH2)6NH2, and one mole of adipic acid, HOOC-(CH2)4-COOH. For this case[1][2]
In this equation
-
- Xn is the number-average value of the degree of polymerization, equal to the average number of monomer units in a polymer molecule.
For the example of nylon-6,6 Xn = 2n (n diamine units and n diacid units). - p is the extent of reaction (or conversion to polymer), defined by
-
- p = (N0-N)/N0, where:
- N0 is the number of molecules present initially
- N is the number of unreacted molecules at time t
- Xn is the number-average value of the degree of polymerization, equal to the average number of monomer units in a polymer molecule.
This equation shows that a high monomer conversion is required to achieve a high degree of polymerization. For example, a monomer conversion, p, of 98% is required for Xn = 50, and p = 99% is required for Xn = 100.
Linear polymers: one monomer in excess
If one monomer is present in stoechiometric excess, then the equation becomes[3]
-
- r is the stoichiometric ratio of reactants, the excess reactant is conventionally the denominator so that r < 1. If neither monomer is in excess, then r = 1 and the equation reduces to the equimolar case above.
The effect of the excess reactant is to reduce the degree of polymerization for a given value of p. In the limit of complete conversion of the limiting reagent monomer, p → 1 and
Thus for a 1% excess of one monomer, r = 0.99 and the limiting degree of polymerization is 199, compared to infinity for the equimolar case. An excess of one reactant can be used to control the degree of polymerization.
Branched polymers: multifunctional monomers
The functionality of a monomer molecule is the number of functional groups which participate in the polymerization. Monomers with functionality greater than two will introduce branching into a polymer, and the degree of polymerization will depend on the average functionality fav per monomer unit. For a system containing N0 molecules initially and equivalent numbers of two functional groups A and B, the total number of functional groups is N0fav.
And the modified Carothers equation is[4][5][6]
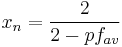 , where p equals to
, where p equals to 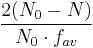
Related equations
Related to the Carothers equation are the following equations (for the simplest case of linear polymers formed from two monomers in equimolar quantities):
where:
-
- Xw is the weight average degree of polymerization,
- Mn is the number average molecular weight,
- Mw is the weight average molecular weight,
- Mo is the molecular weight of the repeating monomer unit,
- PDI is the polydispersity index
The last equation shows that the maximum value of the PDI is 2, which occurs at a monomer conversion of 100% (or p = 1). This is true for step-growth polymerization of linear polymers. For chain-growth polymerization or for branched polymers, the PDI can be much higher.
In practice the average length of the polymer chain is limited by such things as the purity of the reactants, the absence of any side reactions (i.e. high yield), and the viscosity of the medium.
References
- ^ Cowie J.M.G. "Polymers: Chemistry & Physics of Modern Materials (2nd edition, Blackie 1991), p.29
- ^ Rudin Alfred "The Elements of Polymer Science and Engineering", Academic Press 1982, p.171
- ^ Allcock Harry R., Lampe Frederick W. and Mark James E. "Contemporary Polymer Chemistry" (3rd ed., Pearson 2003) p.324
- ^ Carothers, Wallace (1936). "Polymers and polyfunctionality". Transaction of the Faraday Society 32: 39–49. doi:10.1039/TF9363200039.
- ^ Cowie p.40
- ^ Rudin p.170