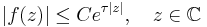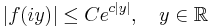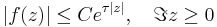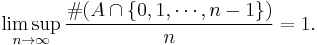Carlson's theorem

Not to be confused with Carleson's theorem

In mathematics, in the area of complex analysis, Carlson's theorem is a uniqueness theorem about a summable expansion of an analytic function. It is typically invoked to defend the uniqueness of a Newton series expansion. Carlson's theorem has generalized analogues for expansions in other bases of polynomials. It is named in honour of Fritz David Carlson.

The theorem may be obtained from the Phragmén–Lindelöf theorem, which is itself an extension of the maximum-modulus theorem.

Contents

Statement of theorem

Assume that

|f(z)| \leq C e^{\tau|z|}, \quad z \in \mathbb{C}
for some C,τ < ∞
|f(iy)| \leq C e^{c|y|}, \quad y \in \mathbb{R}

Then f is identically zero.

Sharpness

First condition

The first condition may be relaxed: it is enough to assume that f is analytic in Re z > 0, continuous in Re z ≥ 0, and satisfies

|f(z)| \leq C e^{\tau|z|}, \quad \Im z \geq 0

for some C,τ < ∞

Second condition

To see that the second condition is sharp, consider the function f(z) = sin(πz). It vanishes on the integers; however, it grows exponentially on the imaginary axis with a growth rate of c = π, and indeed it is not identically zero.

Third condition

A result, due to Rubel (1956), relaxes the condition that f vanish on the integers. Namely, Rubel showed that the conclusion of the theorem remains valid if f vanishes on a subset A ⊂ {0,1,2,...} of upper density 1, meaning that

\limsup_{n \to \infty} \frac{\# \big( A \cap \{0,1,\cdots,n-1\} \big)}{n} = 1.

This condition is sharp, meaning that the theorem fails for sets A of upper density smaller than 1.

References