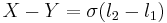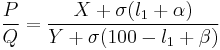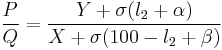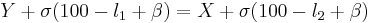Carey Foster bridge

In electronics, the Carey Foster bridge is a bridge circuit used to measure low resistances, or to measure small differences between two large resistances. It was invented by Carey Foster as a variant on the Wheatstone bridge. He first described it in his 1872 paper "On a Modified Form of Wheatstone's Bridge, and Methods of Measuring Small Resistances" (Telegraph Engineer's Journal, 1872-1873, 1, 196).

Contents 1 Use 1.1 To measure σ 2 Theory 3 References

Use

In the diagram to the right, X and Y are resistances to be compared. P and Q are nearly equal resistances, forming the other half of the bridge. The bridge wire EF has a jockey contact D placed along it and is slid until the galvanometer G measures zero. The thick-bordered areas are thick copper busbars of almost zero resistance.

1. Place a known resistance R in position Y.
2. Place the unknown resistance in position X.
3. Place D along the bridge wire EF such as to null the galvanometer. This position (as a percentage of distance from E to F) is l₁.
4. Swap X and Y. Place D at the new null point. This position is l₂.
5. If the resistance of the wire per percentage is σ, then the resistance difference is the resistance of the length of bridge wire between l₁ and l₂:

To measure a low unknown resistance X, replace Y with a copper busbar that can be assumed to be of zero resistance.

In practical use, shunt the galvanometer with a low resistance when the bridge is unbalanced, to avoid burning it out. Only use at full sensitivity when you are close to the null point.

To measure σ

To measure the unit resistance of the bridge wire EF, put a known resistance (e.g. a standard 1 ohm resistance) less than that of the wire as X and a copper busbar of assumed zero resistance as Y.

Theory

Two resistances to be compared, X and Y, are connected in series with the bridge wire. Thus, considered as a Wheatstone bridge, the two resistances are X plus a length of bridge wire, and Y plus the remaining bridge wire. The two remaining arms are the nearly equal resistances P and Q, connected in the inner gaps of the bridge.

Let l₁ be the null point D on the bridge wire EF in percent. α is the unknown left-side extra resistance EX and β is the unknown right-side extra resistance FY, and σ is the resistance per percent length of the bridge wire:

and add 1 to each side:

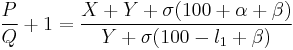      (equation 1)

Now swap X and Y. l₂ is the new null point reading in percent:

and add 1 to each side:

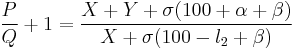      (equation 2)

Equations 1 and 2 have the same left-hand side and the same numerator on the right-hand side, meaning the denominator on the right-hand side must also be equal:

Thus: the difference between X and Y is the resistance of the bridge wire between l₁ and l₂.

The bridge is most sensitive when P, Q, X and Y are all of comparable magnitude.

References

• Carey Foster Bridge (PDF) (Maitreyi College, Delhi University)
• A. H. Fison (1919). "Obituary notices: .... George Carey Foster, 1835–1919; .....". J. Chem. Soc., Trans. 115: 412–427. doi:10.1039/CT9191500408.