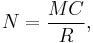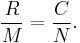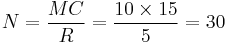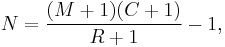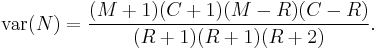Mark and recapture
Mark and recapture is a method commonly used in ecology to estimate population size. This method is most valuable when a researcher fails to detect all individuals present within a population of interest every time that researcher visits the study area. Other names for this method, or closely related methods, include capture-recapture, capture-mark-recapture, mark-recapture, sight-resight, mark-release-recapture, multiple systems estimation and band recovery.
Another major application for these methods is in epidemiology, where they are used to estimate the completeness of ascertainment of disease registers. Typical applications include estimating the number of people needing particular services (i.e. services for children with learning disabilities, services for medically frail elderly living in the community), or with particular conditions(i.e. illegal drug addicts, people infected with HIV, etc.).
Contents |
Typically a researcher visits a study area and uses traps to capture a group of individuals alive. Each of these individuals is marked with a unique identifier (e.g., a numbered tag or band), and then is released unharmed back into the environment. A mark recapture method was first used for ecological study in 1896 by Petersen to estimate plaice, Platichthys platessa, populations.[1]
Sufficient time is allowed to pass for the marked individuals to redistribute themselves among the unmarked population.
Next, the researcher returns and captures another sample of individuals. Some of the individuals in this second sample will have been marked during the initial visit and are now known as recaptures. Other animals captured during the second visit will not have been captured during the first visit to the study area. These unmarked animals usually are given a tag or band during the second visit and then are released.
Population size can be estimated from as few as two visits to the study area. Commonly, more than two visits are made, particularly if estimates of survival or movement are desired. Regardless of the total number of visits, the researcher simply records the date of each capture of each individual. The "capture histories" generated are analyzed mathematically to estimate population size, survival, or movement.
In the epidemiological setting, different sources of patients take the place of the repeated field visits in ecology. To take a concrete example, establishing a register of children with Type 1 diabetes children were identified from hospital admission records, from general practitioners (family doctors), and from the records of the local Diabetes Association. None of these sources had a complete list, but by putting them together it was possible to do two things, first to see how many children were identified in total, and secondly to estimate how many more children with Type 1 diabetes were living in the vital community
Lincoln–Petersen method of analysis
The Lincoln–Petersen method[2] (also known as the Lincoln index) can be used to estimate population size if only two visits are made to the study area. This method assumes that the study population is "closed." In other words, the two visits to the study area are close enough in time so that no individuals die, are born, move into the study area (immigrate) or move out of the study area (emigrate) between visits. The model also assumes that no marks fall off animals between visits to the field site by the researcher, and that the researcher correctly records all marks.
Given those conditions, estimated population size is:
where
- N = Estimate of total population size
- M = Total number of animals captured and marked on the first visit
- C = Total number of animals captured on the second visit
- R = Number of animals captured on the first visit that were then recaptured on the second visit
Adaptation of the Lincoln–Petersen method
It is assumed (Krebs, 1998) that all individuals have the same probability of being captured in the second sample, regardless of whether they were previously captured in the first sample (with only two samples, this assumption cannot be tested directly).
This implies that, in the second sample, the proportion of marked individuals that are caught (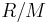 ) should equal the proportion of the total population that is caught (
) should equal the proportion of the total population that is caught (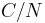 ). For example, if half of the marked individuals were recaptured, it would be assumed that half of the total population was included in the second sample.
). For example, if half of the marked individuals were recaptured, it would be assumed that half of the total population was included in the second sample.
In symbols,
A rearrangement of this gives
the formula used for the Lincoln–Petersen method (Krebs, 1998).
Sample calculation
A biologist wants to estimate the size of a population of turtles in a lake. She captures 10 turtles on her first visit to the lake, and marks their backs with paint. A week later she returns to the lake and captures 15 turtles. Five of these 15 turtles have paint on their backs, indicating that they are recaptured animals.
In this example, the Lincoln–Petersen method estimates that there are 30 turtles in the lake.
A refined form. The Schnabel Method of M-R
Known as the Schnabel Method of M-R. A less biased estimator of population size can be obtained with a modified version of the first formula above:[3]
where, as before,
- N = Estimate of total population size
- M = Total number of animals captured and marked on the first visit
- C = Total number of animals captured on the second visit
- R = Number of animals captured on the first visit that were then recaptured on the second visit
An approximately unbiased variance of N, or var(N), can be estimated as:
More than two visits
The literature on the analysis of capture-recapture studies has blossomed since the early 1990s. There are very elaborate statistical models available for the analysis of these experiments. A simple model which easily accommodates the three source, or the three visit study, is to fit a Poisson regression model. Sophisticated mark-recapture models can be fit using Recapture [1], a package of the Open Source R programming language, or specialized programs such as MARK [2] or M-SURGE [3]. The other related methods which are often used, include Jolly-Seber method (used in open populations and for multiple census estimates) and Schnabel estimates (described above as an expansion to the Lincoln-Petersen method for closed populations). These are described in detail by Sutherland.
Integrated approaches
Modeling mark-recapture data is trending towards a more integrative approach,[4] which combines mark-recapture data with population dynamics models and other types of data. The integrated approach is more computationally demanding, but extracts more information from the data improving parameter and uncertainty estimates.[5]
See also
- German tank problem, for estimation of population size when the elements are numbered
References
- ^ Southwood, T.R.E. & Henderson, P. (2000) Ecological Methods, 3rd edn. Blackwell Science, Oxford.
- ^ Seber, G.A.F.. The Estimation of Animal Abundance and Related Parameters. Caldwel,New Jersey: Blackburn Press. ISBN 1930665555
- ^ Chapman, D.G. (1951). Some properties of the hypergeometric distribution with applications to zoological sample censuses.
- ^ Maunder M.N. (2003) Paradigm shifts in fisheries stock assessment: from integrated analysis to Bayesian analysis and back again. Natural Resource Modeling 16:465-475
- ^ Maunder, M.N. (2001) Integrated Tagging and Catch-at-Age Analysis (ITCAAN). In Spatial Processes and Management of Fish Populations, edited by G.H. Kruse,N. Bez, A. Booth, M.W. Dorn, S. Hills, R.N. Lipcius, D. Pelletier, C. Roy, S.J. Smith, and D. Witherell, Alaska Sea Grant College Program Report No. AK-SG-01-02, University of Alaska Fairbanks, pp. 123-146.
- Besbeas, P; Freeman, S. N., Morgan, B. J. T., Catchpole, E. A. (2002). "Integrating mark-recapture-recovery and census data to estimate animal abundance and demographi parameters.". Biometrics 58 (3): 540–547. doi:10.1111/j.0006-341X.2002.00540.x. PMID 12229988.
- Martin-Löf, P. (1961). "Mortality rate calculations on ringed birds with special reference to the Dunlin Calidris alpina". Arkiv för Zoologi (Zoology files), Kungliga Svenska Vetenskapsakademien (The Royal Swedish Academy of Sciences) Serie 2 Band 13 (21).
- Maunder, M. N. (2004). "Population viability analysis, based on combining integrated, Bayesian, and hierarchical analyses". Acta Oecologica 26: 85–94. doi:10.1016/j.actao.2003.11.008.
- Phillips, C. A.; M. J. Dreslik, J. R. Johnson, and J. E. Petzing (2001). "Application of population estimation to pond breeding salamanders". Transactions of the Illinois Academy of Science 94 (2): 111–118.
- Royle, J. A.; R. M. Dorazio (2008). Hierarchical Modeling and Inference in Ecology. Elsevier. ISBN 1930665555.
- Seber, G.A.F.. The Estimation of Animal Abundance and Related Parameters. Caldwel,New Jersey: Blackburn Press. ISBN 1930665555.
- Schaub, M; Gimenez, O., Sierro, A., and Arlettaz, R (2007). "Use of Integrated Modeling to Enhance Estimates of Population Dynamics Obtained from Limited Data". Conservation Biology 21 (4): 945–955. doi:10.1111/j.1523-1739.2007.00743.x. PMID 17650245.
- Williams, B. K.; J. D. Nichols, and M. J. Conroy (2002). Analysis and Management of Animal Populations. San Diego, California: Academic Press. ISBN 0127544062.
Further reading
- Bonett, D.G., Woodward, J.A., & Bentler, P.M. (1986). "A Linear Model for Estimating the Size of a Closed Population", British Journal of Mathematical and Statistical Psychology, 39, 28-40.
- Evans, M.A., Bonett, D.G., & McDonald, L. (1994). "A General Theory for Analyzing Capture-recapture Data in Closed Populations." Biometrics, 50, 396-405.
- Lincoln, F. C. (1930). "Calculating Waterfowl Abundance on the Basis of Banding Returns". United States Department of Agriculture Circular, 118, 1–4.
- Petersen, C. G. J. (1896). "The Yearly Immigration of Young Plaice Into the Limfjord From the German Sea", Report of the Danish Biological Station (1895), 6, 5–84.
- Schofield, J. R. (2007). "Beyond Defect Removal: Latent Defect Estimation With Capture-Recapture Method", Crosstalk, August, 2007; 27-29.