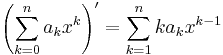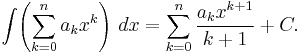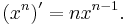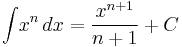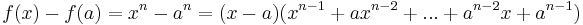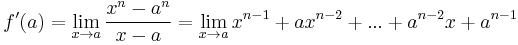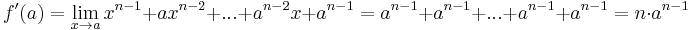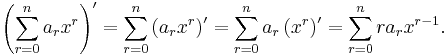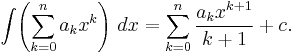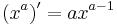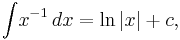Calculus with polynomials

Fundamental theorem
Limits of functions
Continuity
Mean value theorem

Differential calculus
Derivative Change of variables Implicit differentiation Taylor's theorem Related rates Rules and identities: Power rule, Product rule, Quotient rule, Chain rule

Integral calculus
Integral Lists of integrals Improper integrals Integration by: parts, disks, cylindrical shells, substitution, trigonometric substitution, partial fractions, changing order

Vector calculus
Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem

Multivariable calculus
Matrix calculus Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian

In mathematics, polynomials are perhaps the simplest functions used in calculus. Their derivatives and indefinite integrals are given by the following rules:

$\left( \sum^n_{k=0} a_k x^k\right)' = \sum^n_{k=1} ka_kx^{k-1}$

and

$\int\!\left( \sum^n_{k=0} a_k x^k\right)\,dx= \sum^n_{k=0} \frac{a_k x^{k%2B1}}{k%2B1} %2B C .\!$

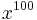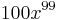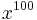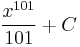Hence, the derivative of $x^{100}$ is $100x^{99}$ and the indefinite integral of $x^{100}$ is $\frac{x^{101}}{101}%2BC$ where C is an arbitrary constant of integration.

This article will state and prove the power rule for differentiation, and then use it to prove these two formulas.

1 Power rule
- 1.1 Proof
2 Differentiation of arbitrary polynomials
3 Generalization
4 References

Power rule

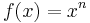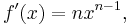The power rule is for polynomials and states that for every integer n, the derivative of $f(x)=x^n \!$ is $f'(x)=nx^{n-1},\!$ that is,

$\left(x^n\right)'=nx^{n-1}.$

The power rule for integration

$\int\! x^n \, dx=\frac{x^{n%2B1}}{n%2B1}%2BC$

for natural n is then an easy consequence. One just needs to take the derivative of this equality and use the power rule and linearity of differentiation on the right-hand side.

Proof

To prove the power rule for differentiation, we use the definition of the derivative as a limit. But first, note the factorization for 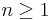$n \geq 1$ :

$f(x)-f(a) = x^n-a^n = (x-a)(x^{n-1}%2Bax^{n-2}%2B...%2Ba^{n-2}x%2Ba^{n-1})$

Using this, we can see that

$f'(a) = \lim_{x\rarr a} \frac{x^n-a^n}{x-a} = \lim_{x\rarr a} x^{n-1}%2Bax^{n-2}%2B...%2Ba^{n-2}x%2Ba^{n-1}$

Since the division has been eliminated and we have a continuous function, we can freely substitute to find the limit:

$f'(a) = \lim_{x\rarr a} x^{n-1}%2Bax^{n-2}%2B...%2Ba^{n-2}x%2Ba^{n-1} = a^{n-1}%2Ba^{n-1}%2B...%2Ba^{n-1}%2Ba^{n-1} = n\cdot a^{n-1}$

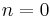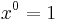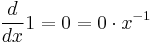The case of $n = 0$ is trivial because $x^0=1$ , so $\frac{d}{dx}1=0=0\cdot x^{-1}$ .

The use of the quotient rule allows the extension of this rule for n as a negative integer, and the use of the laws of exponents and the chain rule allows this rule to be extended to all rational values of n. For an irrational n, a rational approximation is appropriate.

Differentiation of arbitrary polynomials

To differentiate arbitrary polynomials, one can use the linearity property of the differential operator to obtain:

$\left( \sum_{r=0}^n a_r x^r \right)' = \sum_{r=0}^n \left(a_r x^r\right)' = \sum_{r=0}^n a_r \left(x^r\right)' = \sum_{r=0}^n ra_rx^{r-1}.$

Using the linearity of integration and the power rule for integration, one shows in the same way that

$\int\!\left( \sum^n_{k=0} a_k x^k\right)\,dx= \sum^n_{k=0} \frac{a_k x^{k%2B1}}{k%2B1} %2B c.$

Generalization

One can prove that the power rule is valid for any exponent, that is

$\left(x^a\right)' = ax^{a-1}$

for any value a as long as x is in the domain of the functions on the left and right hand sides and a+1 is nonzero. Using this formula, together with

$\int \! x^{-1}\, dx= \ln |x|%2Bc,$

one can differentiate and integrate linear combinations of powers of x which are not necessarily polynomials.

References

Larson, Ron; Hostetler, Robert P.; and Edwards, Bruce H. (2003). Calculus of a Single Variable: Early Transcendental Functions (3rd edition). Houghton Mifflin Company. ISBN 0-618-22307-X.