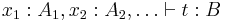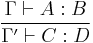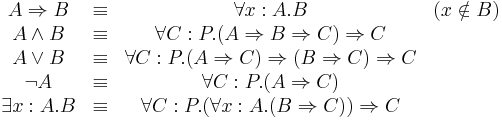Calculus of constructions
The calculus of constructions (CoC) is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.
Contents |
General traits
The CoC is a higher-order typed lambda calculus, initially developed by Thierry Coquand, where types are first-class values. It is thus possible, within the CoC, to define functions from, say, integers to types, types to types as well as functions from integers to integers. Within Barendregt's lambda cube, it is therefore the richest calculus.
The CoC is strongly normalizing, though, by Gödel's incompleteness theorem, it is impossible to prove this property within the CoC since it implies consistency.
The CoC was the basis of the early versions of the Coq proof assistant; later versions were built upon the calculus of inductive constructions, an extension of CoC with native support for inductive datatypes. In the original CoC, inductive datatypes had to be emulated as their polymorphic destructor function.
The basics of the calculus of constructions
The Calculus of Constructions can be considered an extension of the Curry–Howard isomorphism. The Curry–Howard isomorphism associates a term in the simply typed lambda calculus with each natural-deduction proof in intuitionistic propositional logic. The Calculus of Constructions extends this isomorphism to proofs in the full intuitionistic predicate calculus, which includes proofs of quantified statements (which we will also call "propositions").
Terms
A term in the calculus of constructions is constructed using the following rules:
- T is a term (also called Type)
- P is a term (also called Prop, the type of all propositions)
- Variables (x, y, ...) are terms
- If
 and
and  are terms, then so are
are terms, then so are
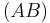
- (
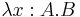 )
) - (
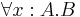 )
)
The calculus of constructions has five kinds of objects:
- proofs, which are terms whose types are propositions
- propositions, which are also known as small types
- predicates, which are functions that return propositions
- large types, which are the types of predicates. (P is an example of a large type)
- T itself, which is the type of large types.
Judgments
The calculus of constructions allows proving typing judgments:
Which can be read as the implication
- If variables
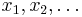 have types
have types 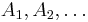 , then term
, then term  has type
has type  .
.
The valid judgments for the calculus of constructions are derivable from a set of inference rules. In the following, we use  to mean a sequence of type assignments
to mean a sequence of type assignments 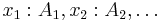 , and we use K to mean either P or T. We will write
, and we use K to mean either P or T. We will write 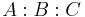 to mean "
to mean " has type
has type  , and
, and  has type
has type  ". We will write
". We will write 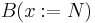 to mean the result of substituting the term
to mean the result of substituting the term  for the variable
for the variable  in the term
in the term  .
.
An inference rule is written in the form
which means
- If
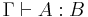 is a valid judgment, then so is
is a valid judgment, then so is 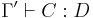
Inference rules for the calculus of constructions
1. 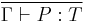
2. 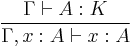
3. 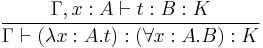
4. 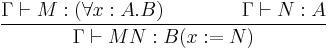
5. 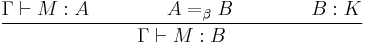
Defining logical operators
The calculus of constructions has very few basic operators: the only logical operator for forming propositions is 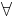 . However, this one operator is sufficient to define all the other logical operators:
. However, this one operator is sufficient to define all the other logical operators:
Defining data types
The basic data types used in computer science can be defined within the Calculus of Constructions:
- Booleans
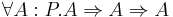
- Naturals
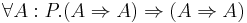
- Product
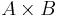
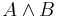
- Disjoint union
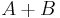
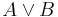
Note that Booleans and Naturals are defined in the same way that in Church encoding. However additional problems raise from propositional extensionality and proof irrelevance [1].
See also
- Curry–Howard isomorphism
- Intuitionistic logic
- Intuitionistic type theory
- Lambda calculus
- Lambda cube
- System F
- Typed lambda calculus
Theorists
References
- Thierry Coquand and Gerard Huet: The Calculus of Constructions. Information and Computation, Vol. 76, Issue 2-3, 1988.
- For a source freely accessible online, see Coquand and Huet: The calculus of constructions. Technical Report 530, INRIA, Centre de Rocquencourt, 1986. Note terminology is rather different. For instance, (
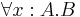 ) is written [x : A] B.
) is written [x : A] B. - M. W. Bunder and Jonathan P. Seldin: Variants of the Basic Calculus of Constructions. 2004.