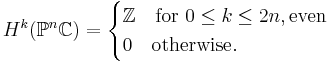CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation.
Contents[hide] |
Formulation
Roughly speaking, a CW-complex is made of basic building blocks called cells. The precise definition prescribes how the cells may be topologically glued together. The C stands for "closure-finite", and the W for "weak topology".
An n-dimensional closed cell is a topological space that is homeomorphic to an n-dimensional closed ball. For example, a simplex is a closed cell, and more generally, a convex polytope is a closed cell. An n-dimensional open cell is a topological space that is homeomorphic to the open ball. A 0-dimensional open (and closed) cell is a singleton space.
A CW complex is a Hausdorff space X together with a partition of X into open cells (of perhaps varying dimension) that satisfies two additional properties:
- For each n-dimensional open cell C in the partition of X, there exists a continuous map f from the n-dimensional closed ball to X such that
- the restriction of f to the interior of the closed ball is a homeomorphism onto the cell C, and
- the image of the boundary of the closed ball is contained in the union of a finite number of elements of the partition, each having cell dimension less than n.
- A subset of X is closed if and only if it meets the closure of each cell in a closed set.
Inductive definition of CW-complexes
If the largest dimension of any of the cells is n, then the CW complex is said to have dimension n. If there is no bound to the cell dimensions then it is said to be infinite-dimensional. The n-skeleton of a CW complex is the union of the cells whose dimension is at most n. If the union of a set of cells is closed, then this union is itself a CW complex, called a subcomplex. Thus the n-skeleton is the largest subcomplex of dimension n or less.
A CW complex is often constructed by defining its skeleta inductively. Begin by taking the 0-skeleton to be a discrete space. Next, attach 1-cells to the 0-skeleton. Here, the 1-cells are attached to points of the 0-skeleton via some continuous map from unit 0-sphere, that is,  . Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundary of the 1-cells into the 1-cells. In general, given the n-1-skeleton and a collection of (abstract) closed n-cells, as above, the n-cells are attached to the n-1-skeleton by some continuous mapping from
. Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundary of the 1-cells into the 1-cells. In general, given the n-1-skeleton and a collection of (abstract) closed n-cells, as above, the n-cells are attached to the n-1-skeleton by some continuous mapping from  , and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.
, and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.
Up to isomorphism every n-dimensional complex can be obtained from its n-1 skeleton in this sense, and thus every finite-dimensional CW complex can be built up by the process above. This is true even for infinite-dimensional complexes, with the understanding that the result of the infinite process is the direct limit of the skeleta: a set is closed in X if and only if it meets each skeleton in a closed set.
Examples
-
- The space
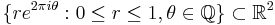 has the homotopy-type of a CW-complex (it is contractible) but it does not admit a CW-decomposition, since it is not locally contractible.
has the homotopy-type of a CW-complex (it is contractible) but it does not admit a CW-decomposition, since it is not locally contractible.
- The space
-
- The Hawaiian earring is an example of a topological space that does not have the homotopy-type of a CW-complex.
-
- The standard CW-structure on the real numbers has 0-skeleton the integers
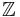 and as 1-cells the intervals
and as 1-cells the intervals ![\{ [n,n%2B1]�: n \in \mathbb Z\}](/2012-wikipedia_en_all_nopic_01_2012/I/7dfb07d729f1ec115a227815978e0476.png) . Similarly, the standard CW-structure on
. Similarly, the standard CW-structure on 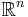 has cubical cells that are products of the 0 and 1-cells from
has cubical cells that are products of the 0 and 1-cells from 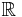 . This is the standard cubical lattice cell structure on
. This is the standard cubical lattice cell structure on 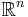 .
.
- The standard CW-structure on the real numbers has 0-skeleton the integers
-
- A polyhedron is naturally a CW-complex.
-
- A graph is a 1-dimensional CW-complex. Trivalent graphs can be considered as generic 1-dimensional CW-complexes. Specifically, if X is a 1-dimensional CW-complex, the attaching map for a 1-cell is a map from a two-point space to X,
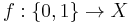 . This map can be perturbed to be disjoint from the 0-skeleton of X if and only if
. This map can be perturbed to be disjoint from the 0-skeleton of X if and only if 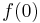 and
and 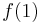 are not 0-valence vertices of X.
are not 0-valence vertices of X.
- A graph is a 1-dimensional CW-complex. Trivalent graphs can be considered as generic 1-dimensional CW-complexes. Specifically, if X is a 1-dimensional CW-complex, the attaching map for a 1-cell is a map from a two-point space to X,
-
- The terminology for a generic 2-dimensional CW-complex is a shadow.[1]
-
- The n-dimensional sphere admits a CW-structure with two cells, one 0-cell and one n-cell. Here the n-cell is attached by the constant mapping from
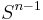 to 0-cell. There is a popular alternative cell decomposition, since the equatorial inclusion
to 0-cell. There is a popular alternative cell decomposition, since the equatorial inclusion 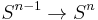 has complement two balls: the upper and lower hemi-spheres. Inductively, this gives
has complement two balls: the upper and lower hemi-spheres. Inductively, this gives 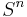 a CW-decomposition with two cells in every dimension k such that
a CW-decomposition with two cells in every dimension k such that 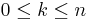 .
.
- The n-dimensional sphere admits a CW-structure with two cells, one 0-cell and one n-cell. Here the n-cell is attached by the constant mapping from
-
- The n-dimensional real projective space admits a CW-structure with one cell in each dimension.
-
- Grassmannian manifolds admit a CW-structure called Schubert cells.
-
- The one-point compactification of a cusped hyperbolic manifold has a canonical CW-decomposition with only one 0-cell (the compactification point) called the Epstein-Penner Decomposition. Such cell decompositions are frequently called ideal polyhedral decompositions and are used in popular computer software, SnapPea.
Homology and cohomology of CW-complexes
Singular homology and cohomology of CW-complexes is readily computable via cellular homology. Moreover, in the category of CW-complexes and cellular maps, cellular homology can be interpreted as a homology theory. To compute an extraordinary (co)homology theory for a CW-complex, the Atiyah-Hirzebruch spectral sequence is the analogue of cellular homology.
Some examples:
-
- For the sphere
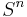 , take the cell decomposition with two cells: a single 0-cell and a single n-cell. The cellular homology chain complex
, take the cell decomposition with two cells: a single 0-cell and a single n-cell. The cellular homology chain complex 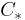 and homology are given by:
and homology are given by:
- For the sphere
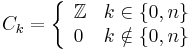
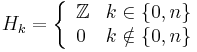 since all the differentials are zero.
since all the differentials are zero.
Alternatively, if we use the equatorial decomposition with two cells in every dimension 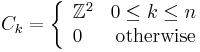 and the differentials are matrices of the form
and the differentials are matrices of the form 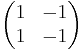 . This gives the same homology computation above, as the chain complex is exact at all terms except
. This gives the same homology computation above, as the chain complex is exact at all terms except 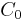 and
and 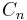 .
.
-
- For
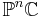 we get similarly
we get similarly
- For
Both of the above examples are particularly simple because the homology is determined by the number of cells—i.e.: the cellular attaching maps have no role in these computations. This is a very special phenomenon and is not indicative of the general case.
Modification of CW-structures
There is a technique, developed by Whitehead, for replacing a CW-complex with a homotopy-equivalent CW-complex which has a simpler CW-decomposition.
Consider, for example, an arbitrary CW-complex. Its 1-skeleton can be fairly complicated, being an arbitrary graph. Now consider a maximal forest F in this graph. Since it is a collection of trees, and trees are contractible, consider the space 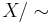 where the equivalence relation is generated by
where the equivalence relation is generated by 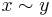 if they are contained in a common tree in the maximal forest F. The quotient map
if they are contained in a common tree in the maximal forest F. The quotient map 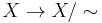 is a homotopy equivalence. Moreover,
is a homotopy equivalence. Moreover, 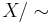 naturally inherits a CW-structure, with cells corresponding to the cells of
naturally inherits a CW-structure, with cells corresponding to the cells of  which are not contained in F. In particular, the 1-skeleton of
which are not contained in F. In particular, the 1-skeleton of 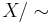 is a disjoint union of wedges of circles.
is a disjoint union of wedges of circles.
Another way of stating the above is that a connected CW-complex can be replaced by a homotopy-equivalent CW-complex whose 0-skeleton consists of a single point.
Consider climbing up the connectivity ladder—assume X is a simply-connected CW-complex whose 0-skeleton consists of a point. Can we, through suitable modifications, replace X by a homotopy-equivalent CW-complex where 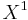 consists of a single point? The answer is yes. The first step is to observe that
consists of a single point? The answer is yes. The first step is to observe that 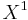 and the attaching maps to construct
and the attaching maps to construct 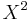 from
from 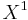 form a group presentation. The Tietze theorem for group presentations states that there is a sequence of moves we can perform to reduce this group presentation to the trivial presentation of the trivial group. There are two Tietze moves:
form a group presentation. The Tietze theorem for group presentations states that there is a sequence of moves we can perform to reduce this group presentation to the trivial presentation of the trivial group. There are two Tietze moves:
- 1) Adding/removing a generator. Adding a generator, from the perspective of the CW-decomposition consists of adding a 1-cell and a 2-cell whose attaching map consists of the new 1-cell and the remainder of the attaching map is in
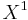 . If we let
. If we let 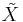 be the corresponding CW-complex
be the corresponding CW-complex  then there is a homotopy-equivalence
then there is a homotopy-equivalence 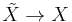 given by sliding the new 2-cell into X.
given by sliding the new 2-cell into X.
- 2) Adding/removing a relation. The act of adding a relation is similar, only one is replacing X by
 where the new 3-cell has an attaching map that consists of the new 2-cell and remainder mapping into
where the new 3-cell has an attaching map that consists of the new 2-cell and remainder mapping into 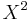 . A similar slide gives a homotopy-equivalence
. A similar slide gives a homotopy-equivalence 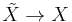 .
.
If a CW-complex X is n-connected one can find a homotopy-equivalent CW-complex 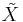 whose n-skeleton
whose n-skeleton 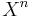 consists of a single point. The argument for
consists of a single point. The argument for 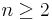 is similar to the
is similar to the 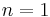 case, only one replaces Tietze moves for the fundamental group presentation by elementary matrix operations for the presentation matrices for
case, only one replaces Tietze moves for the fundamental group presentation by elementary matrix operations for the presentation matrices for 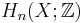 (using the presentation matrices coming from cellular homology. i.e.: one can similarly realize elementary matrix operations by a sequence of addition/removal of cells or suitable homotopies of the attaching maps.
(using the presentation matrices coming from cellular homology. i.e.: one can similarly realize elementary matrix operations by a sequence of addition/removal of cells or suitable homotopies of the attaching maps.
'The' homotopy category
The homotopy category of CW complexes is, in the opinion of some experts, the best if not the only candidate for the homotopy category (for technical reasons the version for pointed spaces is actually used).[2] Auxiliary constructions that yield spaces that are not CW complexes must be used on occasion. One basic result is that the representable functors on the homotopy category have a simple characterisation (the Brown representability theorem).
Properties
-
- CW-complexes are locally contractible.
-
- CW-complexes satisfy the Whitehead theorem -- ie: a map between CW-complexes is a homotopy-equivalence if and only if it induces an isomorphism on all homotopy groups.
-
- The product of two CW-complexes is a CW-complex. The weak topology on this product X×Y is the same as the more familiar product topology on most spaces of interest, but can be finer if X×Y has uncountably many cells and neither X nor Y is locally compact.
-
- The function spaces Hom(X,Y) are not CW-complexes in general but are homotopy equivalent to CW-complexes by a theorem of John Milnor (1959).[3] Actual function spaces occur in the somewhat larger category of compactly generated Hausdorff spaces.
-
- A covering space of a CW complex is also a CW complex.
-
- CW-complexes are paracompact [4] [5]
See also
- The notion of CW-complex has an adaptation to smooth manifolds called a handle decomposition which is closely related to surgery theory.
References
Notes
- ^ Turaev, V. G. (1994), "Quantum invariants of knots and 3-manifolds", De Gruyter Studies in Mathematics (Berlin: Walter de Gruyter & Co.) 18
- ^ For example, the opinion "The class of CW-complexes (or the class of spaces of the same homotopy type as a CW-complex) is the most suitable class of topological spaces in relation to homotopy theory" appears in the article CW-complex of the Springer Encyclopaedia of Mathematics.
- ^ Milnor, John, "On spaces having the homotopy type of a CW-complex" Trans. Amer. Math. Soc. 90 (1959), 272–280.
- ^ Hatcher, Allen, Algebraic topology, Cambridge University Press (2002). ISBN 0-521-79540-0. A free electronic version is available on the author's homepage
- ^ Hatcher, Allen, Vector bundles and K-theory, preliminary version available on the authors homepage
General references
- J. H. C. Whitehead, Combinatorial homotopy. I., Bull. Amer. Math. Soc. 55 (1949), 213–245
- J. H. C. Whitehead, Combinatorial homotopy. II., Bull. Amer. Math. Soc. 55 (1949), 453–496
- Hatcher, Allen, Algebraic topology, Cambridge University Press (2002). ISBN 0-521-79540-0. This textbook defines CW complexes in the first chapter and uses them throughout; includes an appendix on the topology of CW complexes. A free electronic version is available on the author's homepage.
- A. T. Lundell and S. Weingram, The topology of CW complexes, Van Nostrand University Series in Higher Mathematics (1970), ISBN 0-442-04910-2