CM-field

In mathematics, a CM-field is a particular type of number field K, so named for a close connection to the theory of complex multiplication. Another name used is J-field. Specifically, K is a quadratic extension of a totally real field which is totally imaginary, i.e. for which there is no embedding of K into 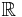$\mathbb R$ .

In other words, there is a subfield 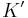$K'$ of K such that K is generated over 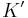$K'$ by a single square root of an element, say β = 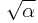$\sqrt{\alpha}$ , in such a way that the minimal polynomial of β over the rational number field 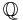$\mathbb Q$ has all its roots non-real complex numbers. For this α should be chosen totally negative, so that for each embedding σ of 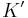$K'$ into the real number field, σ(α) < 0.

Properties

One feature of a CM-field is that complex conjugation on 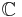$\mathbb C$ induces an automorphism on the field which is independent of the embedding into 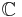$\mathbb C$ . In the notation given, it must change the sign of β.

A number field F is a CM-field if and only if it has a "units defect", i.e. if it contains a proper subfield 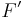$F'$ whose unit group has the same 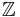$\mathbb Z$ -rank as that of F.^[1] (In fact, 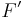$F'$ is the totally real subfield of F mentioned above.) This follows from Dirichlet's unit theorem.

Example

One of the most important examples of a CM-field is the cyclotomic field 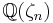$\mathbb Q (\zeta_n)$ , which is generated by a primitive n^th root of unity. It is a totally imaginary quadratic extension of the totally real field 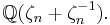$\mathbb Q (\zeta_n %2B\zeta_n^{-1}).$ The latter is the fixed field of complex conjugation, and 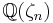$\mathbb Q (\zeta_n)$ is obtained from it by adjoining a square root of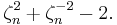 $\zeta_n^2%2B\zeta_n^{-2}-2.$

References

Washington, Lawrence C. (1996). Introduction to Cyclotomic fields (2nd edition ed.). New York: Springer-Verlag. ISBN 0-387-94762-0.

^ Remak, Robert: Über algebraische Zahlkörper mit schwachem Einheitsdefekt. (German) Compositio Math. 12, (1954). 35--80.