Binary search algorithm
| Class | Search algorithm |
|---|---|
| Data structure | Array |
| Worst case performance | O(log n) |
| Best case performance | O(1) |
| Average case performance | O(log n) |
| Worst case space complexity | O(1) |
In computer science, a binary search or half-interval search algorithm finds the position of a specified value (the input "key") within a sorted array[1][2]. At each stage, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been found so its index, or position, is returned. Otherwise, if the sought key is less than the middle element's key, then the algorithm repeats its action on the sub-array to the left of the middle element or, if the input key is greater, on the sub-array to the right. If the remaining array to be searched is reduced to zero, then the key cannot be found in the array and a special "Not found" indication is returned.
A binary search halves the number of items to check with each iteration, so locating an item (or determining its absence) takes logarithmic time. A binary search is a dichotomic divide and conquer search algorithm.
Contents |
Overview
Searching a sorted collection is a common task. A dictionary is a sorted list of word definitions. Given a word, one can find its definition. A telephone book is a sorted list of people's names, addresses, and telephone numbers. Knowing someone's name allows one to quickly find their telephone number and address.
If the list to be searched contains more than a few items (a dozen, say) a binary search will require far fewer comparisons than a linear search, but it imposes the requirement that the list be sorted. Similarly, a hash search can be faster than a binary search but imposes still greater requirements. If the contents of the array are modified between searches, maintaining these requirements may take more time than the searches! And if it is known that some items will be searched for much more often than others, and it can be arranged that these items are at the start of the list, then a linear search may be the best.
Examples
Number guessing game
This rather simple game begins something like "I'm thinking of an integer between forty and sixty inclusive, and to your guesses I'll respond 'High', 'Low', or 'Yes!' as might be the case." Supposing that N is the number of possible values (here, twenty-one as "inclusive" was stated), then at most 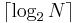 questions are required to determine the number, since each question halves the search space. Note that one less question (iteration) is required than for the general algorithm, since the number is already constrained to be within a particular range.
questions are required to determine the number, since each question halves the search space. Note that one less question (iteration) is required than for the general algorithm, since the number is already constrained to be within a particular range.
Even if the number to guess can be arbitrarily large, in which case there is no upper bound N, The number can be found in at most 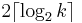 steps (where k is the (unknown) selected number) by first finding an upper bound by repeated doubling. For example, if the number were 11, the following sequence of guesses could be used to find it: 1, 2, 4, 8, 16, 12, 10, 11
steps (where k is the (unknown) selected number) by first finding an upper bound by repeated doubling. For example, if the number were 11, the following sequence of guesses could be used to find it: 1, 2, 4, 8, 16, 12, 10, 11
One could also extend the method to include negative numbers; for example the following guesses could be used to find −13: 0, −1, −2, −4, −8, −16, −12, −14, −13.
Word lists
People typically use a mixture of the binary search and interpolative search algorithms when searching a telephone book, after the initial guess we exploit the fact that the entries are sorted and can rapidly find the required entry. For example when searching for Smith, if Rogers and Thomas have been found, one can flip to a page about halfway between the previous guesses. If this shows Samson, it can be concluded that Smith is somewhere between the Samson and Thomas pages so these can be divided.
Applications to complexity theory
Even if we do not know a fixed range the number k falls in, we can still determine its value by asking 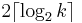 simple yes/no questions of the form "Is k greater than x?" for some number x. As a simple consequence of this, if you can answer the question "Is this integer property k greater than a given value?" in some amount of time then you can find the value of that property in the same amount of time with an added factor of
simple yes/no questions of the form "Is k greater than x?" for some number x. As a simple consequence of this, if you can answer the question "Is this integer property k greater than a given value?" in some amount of time then you can find the value of that property in the same amount of time with an added factor of 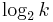 . This is called a reduction, and it is because of this kind of reduction that most complexity theorists concentrate on decision problems, algorithms that produce a simple yes/no answer.
. This is called a reduction, and it is because of this kind of reduction that most complexity theorists concentrate on decision problems, algorithms that produce a simple yes/no answer.
For example, suppose we could answer "Does this n x n matrix have determinant larger than k?" in O(n2) time. Then, by using binary search, we could find the (ceiling of the) determinant itself in O(n2log d) time, where d is the determinant; notice that d is not the size of the input, but the size of the output.
Performance
With each test that fails to find a match at the probed position, the search is continued with one or other of the two sub-intervals, each at most half the size. More precisely, if the number of items, N, is odd then both sub-intervals will contain (N - 1)/2 elements, while if N is even then the two sub-intervals contain N/2 - 1 and N/2 elements.
If the original number of items is N then after the first iteration there will be at most N/2 items remaining, then at most N/4 items, at most N/8 items, and so on. In the worst case, when the value is not in the list, the algorithm must continue iterating until the span has been made empty; this will have taken at most ⌊log2(N) + 1⌋ iterations, where the ⌊ ⌋ notation denotes the floor function that rounds its argument down to an integer. This worst case analysis is tight: for any N there exists a query that takes exactly ⌊log2(N) + 1⌋ iterations. When compared to linear search, whose worst-case behaviour is N iterations, we see that binary search is substantially faster as N grows large. For example, to search a list of one million items takes as many as one million iterations with linear search, but never more than twenty iterations with binary search. However, a binary search can only be performed if the list is in sorted order.
Average performance
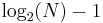 is the expected number of probes in an average successful search, and the worst case is
is the expected number of probes in an average successful search, and the worst case is 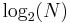 , just one more probe. If the list is empty, no probes at all are made. Thus binary search is a logarithmic algorithm and executes in O(
, just one more probe. If the list is empty, no probes at all are made. Thus binary search is a logarithmic algorithm and executes in O(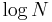 ) time. In most cases it is considerably faster than a linear search. It can be implemented using iteration, or recursion. In some languages it is more elegantly expressed recursively; however, in some C-based languages tail recursion is not eliminated and the recursive version requires more stack space.
) time. In most cases it is considerably faster than a linear search. It can be implemented using iteration, or recursion. In some languages it is more elegantly expressed recursively; however, in some C-based languages tail recursion is not eliminated and the recursive version requires more stack space.
Binary search can interact poorly with the memory hierarchy (i.e. caching), because of its random-access nature. For in-memory searching, if the span to be searched is small, a linear search may have superior performance simply because it exhibits better locality of reference. For external searching, care must be taken or each of the first several probes will lead to a disk seek. A common method is to abandon binary searching for linear searching as soon as the size of the remaining span falls below a small value such as 8 or 16 or even more in recent computers. The exact value depends entirely on the machine running the algorithm.
Notice that for multiple searches with a fixed value for N, then (with the appropriate regard for integer division), the first iteration always selects the middle element at N/2, and the second always selects either N/4 or 3N/4, and so on. Thus if the array's key values are in some sort of slow storage (on a disc file, in virtual memory, not in the cpu's on-chip memory), keeping those three keys in a local array for a special preliminary search will avoid accessing widely separated memory. Escalating to seven or fifteen such values will allow further levels at not much cost in storage. On the other hand, if the searches are frequent and not separated by much other activity, the computer's various storage control features will more or less automatically promote frequently-accessed elements into faster storage.
When multiple binary searches are to be performed for the same key in related lists, fractional cascading can be used to speed up successive searches after the first one.
Extensions
There is no particular requirement that the array being searched has the bounds 1 to N. It is possible to search a specified range, elements first to last instead of 1 to N. All that is necessary is that the initialisation of the bounds be L:=first − 1 and R:=last + 1, then all proceeds as before.
The elements of the list are not necessarily all unique. If one searches for a value that occurs multiple times in the list, the index returned will be of the first-encountered equal element, and this will not necessarily be that of the first, last, or middle element of the run of equal-key elements but will depend on the positions of the values. Modifying the list even in seemingly unrelated ways such as adding elements elsewhere in the list may change the result. To find all equal elements an upward and downward linear search can be carried out from the initial result, stopping each search when the element is no longer equal. Thus, e.g. in a table of cities sorted by country, we can find all cities in a given country.
Several algorithms closely related to or extending binary search exist. For instance, noisy binary search solves the same class of projects as regular binary search, with the added complexity that any given test can return a false value at random. (Usually, the number of such erroneous results are bounded in some way, either in the form of an average error rate, or in the total number of errors allowed per element in the search space.) Optimal algorithms for several classes of noisy binary search problems have been known since the late seventies, and more recently, optimal algorithms for noisy binary search in quantum computers (where several elements can be tested at the same time) have been discovered.
Variations
There are many, and they are easily confused. Also, using a binary search within a sorting method is debatable.
Exclusive or inclusive bounds
The most significant differences are between the "exclusive" and "inclusive" forms of the bounds. In the "exclusive" bound form the span to be searched is (L + 1) to (R − 1), and this may seem clumsy when the span to be searched could be described in the "inclusive" form, as L to R. Although the details differ the two forms are equivalent as can be seen by transforming one version into the other. The inclusive bound form may be attained by replacing all appearances of "L" by "(L − 1)" and "R" by "(R + 1)" then rearranging. Thus, the initialisation of L:=0 becomes (L − 1):=0 or L:=1, and R:=N + 1 becomes (R + 1):=N + 1 or R:=N. So far so good, but note now that the changes to L and R are no longer simply transferring the value of p to L or R as appropriate but now must be (R + 1):=p or R:=p − 1, and (L − 1):=p or L:=p + 1.
Thus, the gain of a simpler initialisation, done once, is lost by a more complex calculation, and which is done for every iteration. If that is not enough, the test for an empty span is more complex also, as compared to the simplicity of checking that the value of p is zero. Nevertheless, the inclusive bound form is found in many publications, such as Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition.
Deferred detection of equality
Because of the syntax difficulties discussed below, so that distinguishing the three states <, =, and > would have to be done with two comparisons, it is possible to use just one comparison and at the end when the span is reduced to zero, equality can be tested for. The solution distinguishes only < from >=.
Midpoint and width
An entirely different variation involves abandoning the L and R pointers in favour of a current position p and a width w where at each iteration, p is adjusted by + or − w and w is halved. Professor Knuth remarks "It is possible to do this, but only if extreme care is paid to the details" – Section 6.2.1, page 414 of The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition, outlines an algorithm, with the further remark "Simpler approaches are doomed to failure!"
Computer use
The algorithm
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky… — Professor Donald Knuth[3]
When Jon Bentley assigned it as a problem in a course for professional programmers, he found that an astounding ninety percent failed to code a binary search correctly after several hours of working on it[4], and another study shows that accurate code for it is only found in five out of twenty textbooks[5]. Furthermore, Bentley's own implementation of binary search, published in his 1986 book Programming Pearls, contains an error that remained undetected for over twenty years.[6]
Numerical difficulties
In a practical implementation, the variables used to represent the indices will be of finite size, hence only capable of representing a finite range of values. For example, 32-bit unsigned integers can only hold values from 0 to 4294967295. Most binary search algorithms use 32-bit signed integers, which can only hold values from -2147483648 to 2147483647. If the binary search algorithm is to operate on large arrays, this has two implications:
- The values
first − 1andlast + 1must both be representable within the finite bounds of the chosen integer type . Therefore, continuing the 32-bit unsigned example, the largest value thatlastmay take is +4294967294, not +4294967295. A problem exists even for the "inclusive" form of the method, as ifx > A(4294967295).Key, then on the final iteration the algorithm will attempt to store 4294967296 intoLand fail. Equivalent issues apply to the lower limit, wherefirst − 1could become negative as when the first element of the array is at index zero. - If the midpoint of the span is calculated as
p := (L + R)/2, then the value(L + R)will exceed the number range iflastis greater than (for unsigned) 4294967295/2 or (for signed) 2147483647/2 and the search wanders toward the upper end of the search space. This can be avoided by performing the calculation asp := (R - L)/2 + L. When the problem arises for signed integers, a more efficient alternative is by performing the calculation asp := (R + L) >>> 1, where>>>denotes the right logical shift operator. For example, this bug existed in Java SDK atArrays.binarySearch()from 1.2 to 5.0 and fixed in 6.0.[7]
Implementations
Iterative
The following incorrect (see notes below) algorithm is slightly modified (to avoid overflow) from Niklaus Wirth's in standard Pascal:[8]
min := 1; max := N; {array size: var A : array [1..N] of integer} repeat mid := (min+max) div 2; if x > A[mid] then min := mid + 1; else max := mid - 1; until (A[mid] = x) or (min > max);
Note: This code assumes 1-based array indexing. For languages that use 0-based indexing (most modern languages), min and max should be initialized to 0 and N-1.
Note 2: The code above does not return a result, nor indicates whether the element was found or not.
Note 3: The code above will not work correctly for empty arrays, because it attempts to access an element before checking to see if min > max.
Note 4: After exiting the loop, the value of mid does not properly indicate whether the desired value was found in the array. One would need to perform one more comparison to determine if the value A[mid] is equal to x.
This code uses inclusive bounds and a three-way test (for early loop termination in case of equality), but with two separate comparisons per iteration. It is not the most efficient solution.
Recursive
A simple, straightforward implementation is tail recursive; it recursively searches the subrange dictated by the comparison:
binary_search(Array[0..N-1], value, low, high):
if (high < low):
return -1 // not found
mid = (low + high) / 2
if (A[mid] > value):
return binary_search(A, value, low, mid-1)
else if (A[mid] < value):
return binary_search(A, value, mid+1, high)
else:
return mid // found
It is invoked with initial low and high values of 0 and N-1.
Language support
Many standard libraries provide a way to do a binary search:
- C provides algorithm function bsearch in its standard library.
- C++'s STL provides algorithm functions
binary_search,lower_boundandupper_bound. - Java offers a set of overloaded
binarySearch()static methods in the classesArraysandCollectionsin the standardjava.utilpackage for performing binary searches on Java arrays and onLists, respectively. They must be arrays of primitives, or the arrays or Lists must be of a type that implements theComparableinterface, or you must specify a customComparatorobject. - Microsoft's .NET Framework 2.0 offers static generic versions of the binary search algorithm in its collection base classes. An example would be
System.Array's methodBinarySearch<T>(T[] array, T value). - Python provides the
bisectmodule. - COBOL can perform binary search on internal tables using the
SEARCH ALLstatement. - Perl can perform a generic binary search using the CPAN module Search::Binary.[9]
- Go's
sortstandard library package contains functionsSearch,SearchInts,SearchFloat64s, andSearchStrings, which implement general binary search, as well as specific implementations for searching slices of integers, floating-point numbers, and strings, respectively.[3] - For Objective-C, the Cocoa framework provides the NSArray -indexOfObject:inSortedRange:options:usingComparator: method in Mac OS X 10.6+. Apple's Core Foundation C framework also contains a CFArrayBSearchValues() function.
See also
- Interpolation search, similar method with better average complexity
- Index (information technology), very fast 'lookup' using an index to directly select an entry
- Branch table, alternative indexed 'lookup' method for decision making
- Self-balancing binary search tree
- Run-time analysis, illustrating binary search method on machines of differing speeds
- Bisection method, the same idea used to solve equations in the real numbers
References
- ^ Introduction to Algorithms, [1], pp15
- ^ http://mathworld.wolfram.com/BinarySearch.html
- ^ Knuth, Donald (1997). The Art of Computer Programming, Volume 3, Sorting and Searching (3rd edition ed.). Addison-Wesley. pp. 409–426. ISBN 0201896850.
- ^ Bentley, Jon (2000) [1986]. Programming Pearls (2nd edition ed.). Addison-Wesley. p. 341. ISBN 0201657880.
- ^ Richard E. Pattis, "Textbook errors in binary searching," SIGCSE Bulletin, 20 (1988), 190–194 cited at Kruse, Robert (1998). Data Structures and Program Design in C++. Prentice Hall. p. 280. ISBN 0137689950.
- ^ Extra, Extra – Read All About It: Nearly All Binary Searches and Mergesorts are Broken, Google Research Blog
- ^ Bug ID: 5045582 (coll) binarySearch() fails for size larger than 1<<30
- ^ Niklaus Wirth: Algorithms + Data Structures = Programs. Prentice-Hall, 1975, ISBN 0-13-022418-9 [2]
- ^ CPAN: Seach::Binary
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.2.1: Searching an Ordered Table, pp. 409–426.
- Kruse, Robert L.: "Data Structures and Program Design in C++", Prentice-Hall, 1999, ISBN 0-13-768995-0, page 280.
- Netty van Gasteren, Wim Feijen. The Binary Search Revisited, AvG127/WF214, 1995. (investigates the foundations of the binary search, debunking the myth that it applies only to sorted arrays)