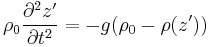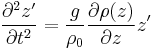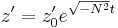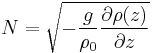Brunt–Väisälä frequency

In atmospheric dynamics, oceanography, and geophysics, the Brunt–Väisälä frequency, or buoyancy frequency, is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. It is named after David Brunt and Vilho Väisälä.

Contents

Derivation for a general fluid

Consider a parcel of (water or gas) that has density of 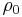\rho_0 and the environment with a density that is a function of height: 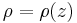\rho = \rho (z). If the parcel is displaced by a small vertical increment 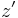z', it will subject to an extra gravitational force against its surroundings of:

\rho_0 \frac{\partial^2 z'}{\partial t^2} = - g (\rho_0- \rho (z'))

g is the gravitational acceleration, and is defined to be positive. We make a Newton's method approximation to 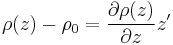\rho (z) - \rho_0 = \frac{\partial \rho (z)}{\partial z} z', and move 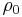\rho_0 to the RHS:

\frac{\partial^2 z'}{\partial t^2} = \frac{g}{\rho_0} \frac{\partial \rho (z)}{\partial z} z'

The above 2nd order differential equation has straightforward solutions of:

z' = z'_0 e^{\sqrt{-N^2} t}\!

where the Brunt–Väisälä frequency N is:

N = \sqrt{- \frac{g}{\rho_0} \frac{\partial \rho (z)}{\partial z}}

For negative 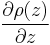\frac{\partial \rho (z)}{\partial z}, z' has oscillating solutions (and N gives our frequency). If it is positive, then there is run away growth – i.e. the fluid is statically unstable.

In meteorology and oceanography

In the atmosphere,

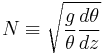N \equiv \sqrt{\frac{g}{\theta}\frac{d\theta}{dz}}, where \theta is potential temperature, g is the local acceleration of gravity, and z is geometric height.

In the ocean where salinity is important, or in fresh water lakes near freezing, where density is not a linear function of temperature,

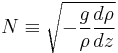N \equiv \sqrt{-\frac{g}{\rho}\frac{d\rho}{dz}}, where \rho, the potential density, depends on both temperature and salinity.

Context

The concept derives from Newton's Second Law when applied to a fluid parcel in the presence of a background stratification (in which the density changes in the vertical). The parcel, perturbed vertically from its starting position, experiences a vertical acceleration. If the acceleration is back towards the initial position, the stratification is said to be stable and the parcel oscillates vertically. In this case, N2 > 0 and the frequency of oscillation is given by N. If the acceleration is away from the initial position (N2 < 0), the stratification is unstable. In this case, overturning or convection generally ensues.

The Brunt–Väisälä frequency relates to internal gravity waves and provides a useful description of atmospheric and oceanic stability.

See also