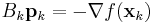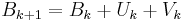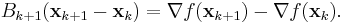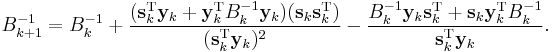BFGS method

In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method is a method for solving nonlinear optimization problems (which lack constraints).

The BFGS method approximates Newton's method, a class of hill-climbing optimization techniques that seeks a stationary point of a (preferably twice continuously differentiable) function: For such problems, a necessary condition for optimality is that the gradient be zero. Newton's method and the BFGS methods need not converge unless the function has a quadratic Taylor expansion near an optimum. These methods use the first and second derivatives. However, BFGS has proven good performance even for non-smooth optimizations.

In quasi-Newton methods, the Hessian matrix of second derivatives need not be evaluated directly. Instead, the Hessian matrix is approximated using rank-one updates specified by gradient evaluations (or approximate gradient evaluations). Quasi-Newton methods are a generalization of the secant method to find the root of the first derivative for multidimensional problems. In multi-dimensions the secant equation does not specify a unique solution, and quasi-Newton methods differ in how they constrain the solution. The BFGS method is one of the most popular members of this class.[1] Also in common use is L-BFGS, which is a limited-memory version of BFGS that is particularly suited to problems with very large numbers of variables (like >1000). The BFGS-B[2] variant handles simple box constraints.

Contents

Rationale

The search direction pk at stage k is given by the solution of the analogue of the Newton equation

B_k \mathbf{p}_k = - \nabla f(\mathbf{x}_k)

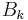where B_k is an approximation to the Hessian matrix which is updated iteratively at each stage, and 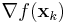\nabla f(\mathbf{x}_k) is the gradient of the function evaluated at xk. A line search in the direction pk is then used to find the next point xk+1. Instead of requiring the full Hessian matrix at the point xk+1 to be computed as Bk+1, the approximate Hessian at stage k is updated by the addition of two matrices.

B_{k%2B1}=B_k%2BU_k%2BV_k\,\!

Both Uk and Vk are symmetric rank-one matrices but have different (matrix) bases. The symmetric rank one assumption here means that we may write

C=\mathbf{a}\mathbf{b}^\mathrm{T}

So equivalently, Uk and Vk construct a rank-two update matrix which is robust against the scale problem often suffered in the gradient descent searching (e.g., in Broyden's method).

The quasi-Newton condition imposed on this update is

B_{k%2B1} (\mathbf{x}_{k%2B1}-\mathbf{x}_k ) = \nabla f(\mathbf{x}_{k%2B1}) -\nabla f(\mathbf{x}_k ).

Algorithm

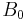From an initial guess \mathbf{x}_0 and an approximate Hessian matrix B_0 the following steps are repeated until x converges to the solution.

  1. Obtain a direction 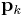\mathbf{p}_k by solving: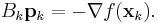 B_k \mathbf{p}_k = -\nabla f(\mathbf{x}_k).
  2. Perform a line search to find an acceptable stepsize 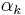\alpha_k in the direction found in the first step, then update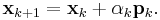 \mathbf{x}_{k%2B1} = \mathbf{x}_k %2B \alpha_k\mathbf{p}_k.
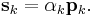
  3. Set \mathbf{s}_k=\alpha_k \mathbf{p}_k.
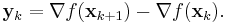
  4. \mathbf{y}_k = {\nabla f(\mathbf{x}_{k%2B1}) - \nabla f(\mathbf{x}_k)}.
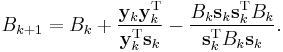
  5. B_{k%2B1} = B_k %2B \frac{\mathbf{y}_k \mathbf{y}_k^{\mathrm{T}}}{\mathbf{y}_k^{\mathrm{T}} \mathbf{s}_k} - \frac{B_k \mathbf{s}_k \mathbf{s}_k^{\mathrm{T}} B_k }{\mathbf{s}_k^{\mathrm{T}} B_k \mathbf{s}_k}.

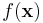f(\mathbf{x}) denotes the objective function to be minimized. Convergence can be checked by observing the norm of the gradient, 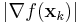\left|\nabla f(\mathbf{x}_k)\right|. Practically, 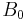B_0 can be initialized with 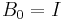B_0 = I, so that the first step will be equivalent to a gradient descent, but further steps are more and more refined by 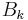B_{k}, the approximation to the Hessian.

The first step of the algorithm is carried out using the inverse of the matrix 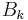B_k, which is usually obtained efficiently by applying the Sherman–Morrison formula to the fifth line of the algorithm, giving

B_{k%2B1}^{-1} = B_k^{-1} %2B \frac{(\mathbf{s}_k^{\mathrm{T}}\mathbf{y}_k%2B\mathbf{y}_k^{\mathrm{T}} B_k^{-1} \mathbf{y}_k)(\mathbf{s}_k \mathbf{s}_k^{\mathrm{T}})}{(\mathbf{s}_k^{\mathrm{T}} \mathbf{y}_k)^2} - \frac{B_k^{-1} \mathbf{y}_k \mathbf{s}_k^{\mathrm{T}} %2B \mathbf{s}_k \mathbf{y}_k^{\mathrm{T}}B_k^{-1}}{\mathbf{s}_k^{\mathrm{T}} \mathbf{y}_k}.

In statistical estimation problems (such as maximum likelihood or Bayesian inference), credible intervals or confidence intervals for the solution can be estimated from the inverse of the final Hessian matrix. However, these quantities are technically defined by the true Hessian matrix, and the BFGS approximation may not converge to the true Hessian matrix.

Implementations

In the Matlab Optimization Toolbox, the fminunc function uses BFGS with cubic line search when the problem size is set to "medium scale." The GSL implements BFGS as gsl_multimin_fdfminimizer_vector_bfgs2. In SciPy, the scipy.optimize.fmin_bfgs function implements BFGS. It is also possible to run BFGS using any of the L-BFGS algorithms by setting the parameter L to a very large number.

See also

Notes

  1. ^ Nocedal & Wright (2006), page 24
  2. ^ R. H. Byrd, P. Lu and J. Nocedal. A Limited Memory Algorithm for Bound Constrained Optimization (1995), SIAM Journal on Scientific and Statistical Computing, 16, 5, pp. 1190–1208.

Bibliography

Optimization: Algorithms, methods, and heuristics
Categories (Algorithms · Methods · Heuristics) · Software