Branches of physics

Further information: Classical physics, Modern physics, Topic outline of physics

Physics deals with a wide variety of systems, there are certain theories that are used by all physicists. Each of these theories were experimentally tested numerous times and found correct as an approximation of Nature (within a certain domain of validity). For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These theories continue to be areas of active research; for instance, a remarkable aspect of classical mechanics known as chaos was discovered in the 20th century, three centuries after the original formulation of classical mechanics by Isaac Newton (1642–1727). These "central theories" are important tools for research into more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.

Contents

Classical mechanics

Main article: Classical mechanics

Classical mechanics is a model data of the physics of forces acting upon bodies. It is often referred to as "Newtonian mechanics" after Isaac Newton and his laws of motion. Mechanics is subdivided into statics, which models objects at rest, kinematics, which models objects in motion, and dynamics, which models objects subjected to forces. The classical mechanics of continuous and deformable objects is continuum mechanics, which can itself be broken down into solid mechanics and fluid mechanics according to the state of matter being studied. The latter, the mechanics of liquids and gases, includes hydrostatics, hydrodynamics, pneumatics, aerodynamics, and other fields.

An important concept of mechanics is the identification of conserved energy and momentum, which lead to the Lagrangian and Hamiltonian reformulations of Newton's laws. Liouville's theorem for statistical and Hamiltonian mechanics is a classical nineteenth century result which describes the behavior of the phase space distribution function. Liouville's theorem has a suggestive formulation, the Poisson bracket, which encodes Hamilton's equations of classical mechanics, and has analogies with the commutator in quantum mechanics.

A relatively recent result of considerations concerning the dynamics of nonlinear systems is chaos theory, the study of systems in which small changes in a variable may have large effects.

Thermodynamics and statistical mechanics

Main articles: Thermodynamics and Statistical mechanics

The first chapter of The Feynman Lectures on Physics is about the existence of atoms, which Feynman considered to be the most compact statement of physics, from which science could easily result even if all other knowledge was lost.[1] By modeling matter as collections of hard spheres, it is possible to describe the kinetic theory of gases, upon which classical thermodynamics is based.

Thermodynamics studies the effects of changes in temperature, pressure, and volume on physical systems at the macroscopic scale, and the transfer of energy as heat.[2][3] Historically, thermodynamics developed out of need to increase the efficiency of early steam engines.[4]

The starting point for most thermodynamic considerations are the laws of thermodynamics, which postulate that energy can be exchanged between physical systems as heat or work.[5] They also postulate the existence of a quantity named entropy, which can be defined for any system.[6] In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of system and surroundings. A system is composed of particles, whose average motions define its properties, which in turn are related to one another through equations of state. Properties can be combined to express internal energy and thermodynamic potentials, which are useful for determining conditions for equilibrium and spontaneous processes.

Electromagnetism

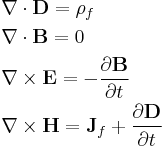\begin{align} &\nabla \cdot \mathbf{D} = \rho_f \\ &\nabla \cdot \mathbf{B} = 0 \\ &\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B} }{\partial t} \\ &\nabla \times \mathbf{H} = \mathbf{J}_f %2B \frac{\partial \mathbf{D} }{\partial t} \end{align}
Maxwell's equations of electromagnetism
Main article: Electromagnetism
See also: Optics

Electromagnetism describes the interaction of charged particles with electric and magnetic fields. It can be divided into electrostatics, the study of interactions between charges at rest, and electrodynamics, the study of interactions between moving charges and radiation. The classical theory of electromagnetism is based on the Lorentz force law and Maxwell's equations. Light is an oscillating electromagnetic field that is radiated from accelerating charged particles. Thus, all of optics, the study of the nature and propagation of light, can be reduced to electromagnetic interactions. Two major fields of optics are geometric optics or "classical optics", and physical optics which studies the electromagnetic properties of light to achieve greater understanding of phenomena such as interference, diffraction, and polarization.

A more recent development is quantum electrodynamics, which incorporates the laws of quantum theory in order to explain the interaction of electromagnetic radiation with matter. Relativistic electrodynamics accounts for relativistic corrections to the motions of charged particles when their speeds approach the speed of light. It applies to phenomena involved with particle accelerators and electron tubes carrying high voltages and currents.

Relativity

Main articles: Special relativity and General relativity

The special theory of relativity enjoys a relationship with electromagnetism and mechanics; that is, the principle of relativity and the principle of stationary action in mechanics can be used to derive Maxwell's equations,[7][8] and vice versa.

The theory of special relativity was proposed in 1905 by Albert Einstein in his article "On the Electrodynamics of Moving Bodies". The title of the article refers to the fact that special relativity resolves an inconsistency between Maxwell's equations and classical mechanics. The theory is based on two postulates: (1) that the mathematical forms of the laws of physics are invariant in all inertial systems; and (2) that the speed of light in a vacuum is constant and independent of the source or observer. Reconciling the two postulates requires a unification of space and time into the frame-dependent concept of spacetime.

General relativity is the geometrical theory of gravitation published by Albert Einstein in 1915/16.[9][10] It unifies special relativity, Newton's law of universal gravitation, and the insight that gravitation can be described by the curvature of space and time. In general relativity, the curvature of space-time is produced by the energy of matter and radiation.

Quantum mechanics

Main article: Quantum mechanics

Quantum mechanics is the branch of physics treating atomic and subatomic systems and their interaction with radiation. It is based on the observation that all forms of energy are released in discrete units or bundles called "quanta". Remarkably, quantum theory typically permits only probable or statistical calculation of the observed features of subatomic particles, understood in terms of wavefunctions. The Schrödinger equation plays the role in quantum mechanics that Newton's laws and conservation of energy serve in classical mechanics — i.e., it predicts the future behavior of a dynamic system — and is a wave equation that is used to solve for wavefunctions.

For example, the light, or electromagnetic radiation emitted or absorbed by an atom has only certain frequencies (or wavelengths), as can be seen from the line spectrum associated with the chemical element represented by that atom. The quantum theory shows that those frequencies correspond to definite energies of the light quanta, or photons, and result from the fact that the electrons of the atom can have only certain allowed energy values, or levels; when an electron changes from one allowed level to another, a quantum of energy is emitted or absorbed whose frequency is directly proportional to the energy difference between the two levels. The photoelectric effect further confirmed the quantization of light.

In 1924, Louis de Broglie proposed that not only do light waves sometimes exhibit particle-like properties, but particles may also exhibit wavelike properties. Two different formulations of quantum mechanics were presented following de Broglie’s suggestion. The wave mechanics of Erwin Schrödinger (1926) involves the use of a mathematical entity, the wave function, which is related to the probability of finding a particle at a given point in space. The matrix mechanics of Werner Heisenberg (1925) makes no mention of wave functions or similar concepts but was shown to be mathematically equivalent to Schrödinger’s theory. A particularly important discovery of the quantum theory is the uncertainty principle, enunciated by Heisenberg in 1927, which places an absolute theoretical limit on the accuracy of certain measurements; as a result, the assumption by earlier scientists that the physical state of a system could be measured exactly and used to predict future states had to be abandoned. Quantum mechanics was combined with the theory of relativity in the formulation of Paul Dirac. Other developments include quantum statistics, quantum electrodynamics, concerned with interactions between charged particles and electromagnetic fields; and its generalization, quantum field theory.

Interdisciplinary fields

To the interdisciplinary fields, which define partially sciences of their own, belong e.g. the

Summary

The table below lists the core theories along with many of the concepts they employ.

Theory Major subtopics Concepts
Classical mechanics Newton's laws of motion, Lagrangian mechanics, Hamiltonian mechanics, Kinematics, Statics, Dynamics, Chaos theory, Acoustics, Fluid dynamics, Continuum mechanics Density, Dimension, Gravity, Space, Time, Motion, Length, Position, Velocity, Acceleration, Galilean invariance, Mass, Momentum, Impulse, Force, Energy, Angular velocity, Angular momentum, Moment of inertia, Torque, Conservation law, Harmonic oscillator, Wave, Work, Power, Lagrangian, Hamiltonian, Tait-Bryan angles, Euler angles
Electromagnetism Electrostatics, Electrodynamics, Electricity, Magnetism, Magnetostatics, Maxwell's equations, Optics Capacitance, Electric charge, Current, Electrical conductivity, Electric field, Electric permittivity, Electric potential, Electrical resistance, Electromagnetic field, Electromagnetic induction, Electromagnetic radiation, Gaussian surface, Magnetic field, Magnetic flux, Magnetic monopole, Magnetic permeability
Thermodynamics and Statistical mechanics Heat engine, Kinetic theory Boltzmann's constant, Conjugate variables, Enthalpy, Entropy, Equation of state, Equipartition theorem, Thermodynamic free energy, Heat, Ideal gas law, Internal energy, Laws of thermodynamics, Maxwell relations, Irreversible process, Ising model, Mechanical action, Partition function, Pressure, Reversible process, Spontaneous process, State function, Statistical ensemble, Temperature, Thermodynamic equilibrium, Thermodynamic potential, Thermodynamic processes, Thermodynamic state, Thermodynamic system, Viscosity, Volume, Work, Granular material
Quantum mechanics Path integral formulation, Scattering theory, Schrödinger equation, Quantum field theory, Quantum statistical mechanics Adiabatic approximation, Blackbody radiation, Correspondence principle, Free particle, Hamiltonian, Hilbert space, Identical particles, Matrix Mechanics, Planck's constant, Observer effect, Operators, Quanta, Quantization, Quantum entanglement, Quantum harmonic oscillator, Quantum number, Quantum tunneling, Schrödinger's cat, Dirac equation, Spin, Wavefunction, Wave mechanics, Wave-particle duality, Zero-point energy, Pauli Exclusion Principle, Heisenberg Uncertainty Principle
Relativity Special relativity, General relativity, Einstein field equations Covariance, Einstein manifold, Equivalence principle, Four-momentum, Four-vector, General principle of relativity, Geodesic motion, Gravity, Gravitoelectromagnetism, Inertial frame of reference, Invariance, Length contraction, Lorentzian manifold, Lorentz transformation, Mass-energy equivalence, Metric, Minkowski diagram, Minkowski space, Principle of Relativity, Proper length, Proper time, Reference frame, Rest energy, Rest mass, Relativity of simultaneity, Spacetime, Special principle of relativity, Speed of light, Stress-energy tensor, Time dilation, Twin paradox, World line

References

  1. ^ R. P. Feynman, R. B. Leighton, M. Sands (1963), The Feynman Lectures on Physics, ISBN 0-201-02116-1 Hard-cover. p.1-1 Feynman begins with the atomic hypothesis, as his most compact statement of all scientific knowledge: "If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed on to the next generations ..., what statement would contain the most information in the fewest words? I believe it is ... that all things are made up of atoms – little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. ..." vol. I p. I–2
  2. ^ Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6. 
  3. ^ Clark, John, O.E. (2004). The Essential Dictionary of Science. Barnes & Noble Books. ISBN 0-7607-4616-8. 
  4. ^ Clausius, Ruldolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff's Annalen der Physick, LXXIX (Dover Reprint). ISBN 0-486-59065-8. 
  5. ^ Van Ness, H.C. (1969). Understanding Thermodynamics. Dover Publications, Inc.. ISBN 0-486-63277-6. 
  6. ^ Dugdale, J.S. (1998). Entropy and its Physical Meaning. Taylor and Francis. ISBN 0-7484-0569-0. 
  7. ^ Landau and Lifshitz (1951, 1962), The Classical Theory of Fields, Library of Congress Card Number 62-9181, Chapters 1–4 (3rd edition is ISBN 0080160190)
  8. ^ Corson and Lorrain, Electromagnetic Fields and Waves ISBN 0716718235
  9. ^ Einstein, Albert (November 25, 1915). "Die Feldgleichungen der Gravitation". Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844–847. http://nausikaa2.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.x.cgi?dir=6E3MAXK4&step=thumb. Retrieved 2006-09-12. 
  10. ^ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik. http://www.alberteinstein.info/gallery/gtext3.html. Retrieved 2006-09-03.