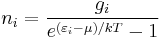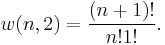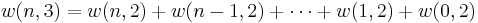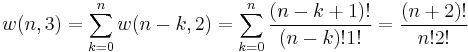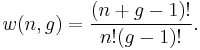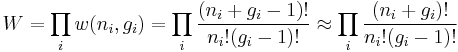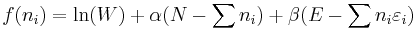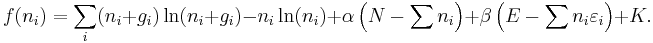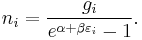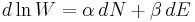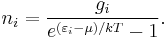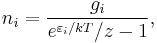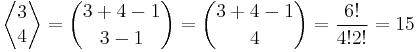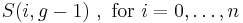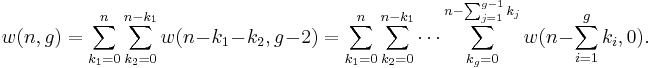Bose–Einstein statistics
| Statistical mechanics |
|---|
| Thermodynamics · Kinetic theory |
In statistical mechanics, Bose–Einstein statistics (or more colloquially B–E statistics) determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.
Contents |
Concept
Fermi–Dirac and Bose–Einstein statistics apply when quantum effects are important and the particles are "indistinguishable". Quantum effects appear if the concentration of particles satisfies N/V ≥ nq. Here nq is the quantum concentration, for which the interparticle distance is equal to the thermal de Broglie wavelength, so that the wavefunctions of the particles are touching but not overlapping. Fermi–Dirac statistics apply to fermions (particles that obey the Pauli exclusion principle), and Bose–Einstein statistics apply to bosons. As the quantum concentration depends on temperature; most systems at high temperatures obey the classical (Maxwell–Boltzmann) limit unless they have a very high density, as for a white dwarf. Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics at high temperature or at low concentration.
Bosons, unlike fermions, are not subject to the Pauli exclusion principle: an unlimited number of particles may occupy the same state at the same time. This explains why, at low temperatures, bosons can behave very differently from fermions; all the particles will tend to congregate at the same lowest-energy state, forming what is known as a Bose–Einstein condensate.
B–E statistics was introduced for photons in 1924 by Bose and generalized to atoms by Einstein in 1924-25.
The expected number of particles in an energy state i for B–E statistics is
with εi > μ and where ni is the number of particles in state i, gi is the degeneracy of state i, εi is the energy of the ith state, μ is the chemical potential, k is the Boltzmann constant, and T is absolute temperature.
This reduces to the Rayleigh-Jeans distribution for 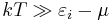 , namely
, namely 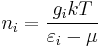 .
.
History
While presenting a lecture at the University of Dhaka on the theory of radiation and the ultraviolet catastrophe, Satyendra Nath Bose a Bengali scientist, intended to show his students that the contemporary theory was inadequate, because it predicted results not in accordance with experimental results. During this lecture, Bose committed an error in applying the theory, which unexpectedly gave a prediction that agreed with the experiment (he later adapted this lecture into a short article called Planck's Law and the Hypothesis of Light Quanta).
The error was a simple mistake—similar to arguing that flipping two fair coins will produce two heads one-third of the time—that would appear obviously wrong to anyone with a basic understanding of statistics. However, the results it predicted agreed with experiment, and Bose realized it might not be a mistake at all. He for the first time took the position that the Maxwell–Boltzmann distribution would not be true for microscopic particles where fluctuations due to Heisenberg's uncertainty principle will be significant. Thus he stressed the probability of finding particles in the phase space, each state having volume h³, and discarding the distinct position and momentum of the particles.
Physics journals refused to publish Bose's paper. Various editors ignored his findings, contending that he had presented them with a simple mistake. Discouraged, he wrote to Albert Einstein, who immediately agreed with him. His theory finally achieved respect when Einstein sent his own paper in support of Bose's to Zeitschrift für Physik, asking that they be published together. This was done in 1924. Bose had earlier translated Einstein's theory of General Relativity from German to English.
The reason Bose's "mistake" produced accurate results was that since photons are indistinguishable from each other, one cannot treat any two photons having equal energy as being two distinct identifiable photons. By analogy, if in an alternate universe coins were to behave like photons and other bosons, the probability of producing two heads would indeed be one-third (tail-head = head-tail). Bose's "error" is now called Bose–Einstein statistics.
Einstein adopted the idea and extended it to atoms. This led to the prediction of the existence of phenomena which became known as Bose-Einstein condensate, a dense collection of bosons (which are particles with integer spin, named after Bose), which was demonstrated to exist by experiment in 1995.
A derivation of the Bose–Einstein distribution
Suppose we have a number of energy levels, labeled by index 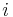 , each level having energy
, each level having energy 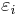 and containing a total of
and containing a total of 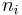 particles. Suppose each level contains
particles. Suppose each level contains 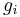 distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy. The value of
distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy. The value of 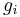 associated with level
associated with level 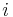 is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
Let 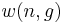 be the number of ways of distributing
be the number of ways of distributing 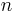 particles among the
particles among the 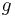 sublevels of an energy level. There is only one way of distributing
sublevels of an energy level. There is only one way of distributing 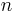 particles with one sublevel, therefore
particles with one sublevel, therefore 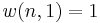 . It is easy to see that there are
. It is easy to see that there are 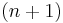 ways of distributing
ways of distributing 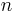 particles in two sublevels which we will write as:
particles in two sublevels which we will write as:
With a little thought (see Notes below) it can be seen that the number of ways of distributing 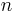 particles in three sublevels is
particles in three sublevels is
so that
where we have used the following theorem involving binomial coefficients:
Continuing this process, we can see that 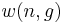 is just a binomial coefficient (See Notes below)
is just a binomial coefficient (See Notes below)
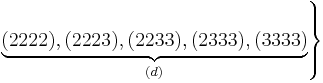
For example, the population numbers for two particles in three sublevels are 200, 110, 101, 020, 011, or 002 for a total of six which equals 4!/(2!2!). The number of ways that a set of occupation numbers 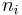 can be realized is the product of the ways that each individual energy level can be populated:
can be realized is the product of the ways that each individual energy level can be populated:
where the approximation assumes that 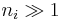 .
.
Following the same procedure used in deriving the Maxwell–Boltzmann statistics, we wish to find the set of 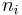 for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of
for which W is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of 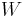 and
and 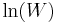 occur at the value of
occur at the value of 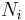 and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers forming the function:
and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers forming the function:
Using the 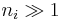 approximation and using Stirling's approximation for the factorials
approximation and using Stirling's approximation for the factorials 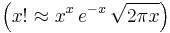 gives
gives
Where K is the sum of a number of terms which are not functions of the 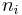 . Taking the derivative with respect to
. Taking the derivative with respect to 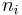 , and setting the result to zero and solving for
, and setting the result to zero and solving for 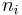 , yields the Bose–Einstein population numbers:
, yields the Bose–Einstein population numbers:
By a process similar to that outlined in the Maxwell-Boltzmann statistics article, it can be seen that:
which, using Boltzmann's famous relationship 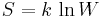 becomes a statement of the second law of thermodynamics at constant volume, and it follows that
becomes a statement of the second law of thermodynamics at constant volume, and it follows that 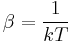 and
and 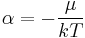 where S is the entropy,
where S is the entropy,  is the chemical potential, k is Boltzmann's constant and T is the temperature, so that finally:
is the chemical potential, k is Boltzmann's constant and T is the temperature, so that finally:
Note that the above formula is sometimes written:
where 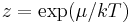 is the absolute activity.
is the absolute activity.
Notes
A much simpler way to think of Bose–Einstein distribution function is to consider that n particles are denoted by identical balls and g shells are marked by g-1 line partitions. It is clear that the permutations of these n balls and g-1 partitions will give different ways of arranging bosons in different energy levels.
Say, for 3(=n) particles and 3(=g) shells, therefore (g-1)=2, the arrangement may be like
|..|. or ||... or |.|.. etc.
Hence the number of distinct permutations of n + (g-1) objects which have n identical items and (g-1) identical items will be:
(n+g-1)!/n!(g-1)!
OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein (B–E) distribution for beginners. The enumeration of cases (or ways) in the B–E distribution can be recast as follows. Consider a game of dice throwing in which there are 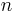 dice, with each die taking values in the set
dice, with each die taking values in the set  , for
, for 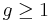 . The constraints of the game are that the value of a die
. The constraints of the game are that the value of a die 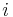 , denoted by
, denoted by 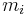 , has to be greater than or equal to the value of die
, has to be greater than or equal to the value of die  , denoted by
, denoted by 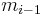 , in the previous throw, i.e.,
, in the previous throw, i.e., 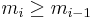 . Thus a valid sequence of die throws can be described by an n-tuple
. Thus a valid sequence of die throws can be described by an n-tuple 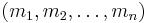 , such that
, such that 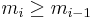 . Let
. Let 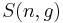 denote the set of these valid n-tuples:
denote the set of these valid n-tuples:
-
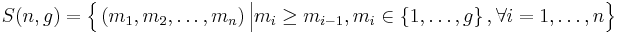
(1)
Then the quantity 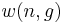 (defined above as the number of ways to distribute
(defined above as the number of ways to distribute 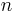 particles among the
particles among the 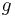 sublevels of an energy level) is the cardinality of
sublevels of an energy level) is the cardinality of 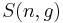 , i.e., the number of elements (or valid n-tuples) in
, i.e., the number of elements (or valid n-tuples) in 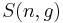 . Thus the problem of finding an expression for
. Thus the problem of finding an expression for 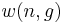 becomes the problem of counting the elements in
becomes the problem of counting the elements in 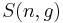 .
.
Example n = 4, g = 3:
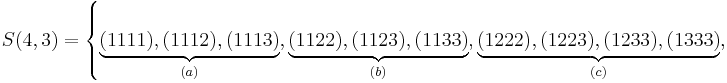
-
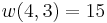 (there are
(there are 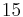 elements in
elements in 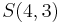 )
)
Subset 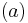 is obtained by fixing all indices
is obtained by fixing all indices 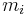 to
to 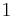 , except for the last index,
, except for the last index, 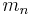 , which is incremented from
, which is incremented from 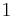 to
to 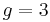 . Subset
. Subset 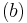 is obtained by fixing
is obtained by fixing 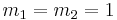 , and incrementing
, and incrementing 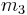 from
from  to
to 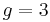 . Due to the constraint
. Due to the constraint 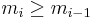 on the indices in
on the indices in 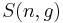 , the index
, the index 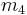 must automatically take values in
must automatically take values in 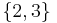 . The construction of subsets
. The construction of subsets 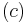 and
and 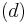 follows in the same manner.
follows in the same manner.
Each element of 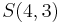 can be thought of as a multiset of cardinality
can be thought of as a multiset of cardinality 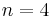 ; the elements of such multiset are taken from the set
; the elements of such multiset are taken from the set 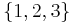 of cardinality
of cardinality 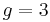 , and the number of such multisets is the multiset coefficient
, and the number of such multisets is the multiset coefficient
- Why "{3 + 4 - 1 \choose 3-1}"="{3 + 4 - 1 \choose 4}"? I Think you should write "\choose 3+1" instead of "\choose 3-1"
More generally, each element of 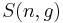 is a multiset of cardinality
is a multiset of cardinality 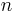 (number of dice) with elements taken from the set
(number of dice) with elements taken from the set  of cardinality
of cardinality 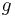 (number of possible values of each die), and the number of such multisets, i.e.,
(number of possible values of each die), and the number of such multisets, i.e., 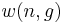 is the multiset coefficient
is the multiset coefficient
-
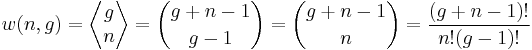
(2)
which is exactly the same as the formula for 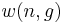 , as derived above with the aid of a theorem involving binomial coefficients, namely
, as derived above with the aid of a theorem involving binomial coefficients, namely
-

(3)
To understand the decomposition
-
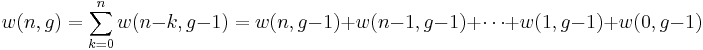
(4)
or for example, 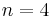 and
and 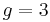
let us rearrange the elements of 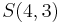 as follows
as follows
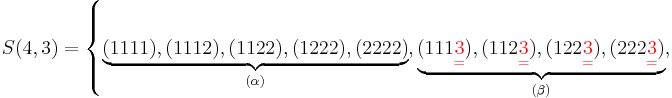
-
-
-
 .
.
-
-
-
Clearly, the subset 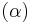 of
of 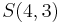 is the same as the set
is the same as the set
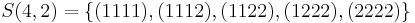 .
.
By deleting the index 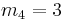 (shown in red with double underline) in the subset
(shown in red with double underline) in the subset 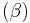 of
of 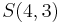 , one obtains the set
, one obtains the set
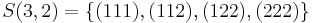 .
.
In other words, there is a one-to-one correspondence between the subset 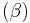 of
of 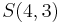 and the set
and the set 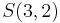 . We write
. We write
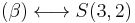 .
.
Similarly, it is easy to see that
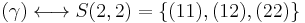
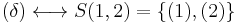
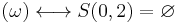 (empty set).
(empty set).
Thus we can write
or more generally,
-
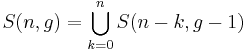 ;
;(5)
and since the sets
are non-intersecting, we thus have
-
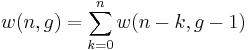 ,
,(6)
with the convention that
-
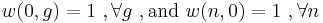 .
.
(7)
Continuing the process, we arrive at the following formula
Using the convention (7)2 above, we obtain the formula
-
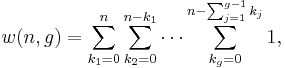
(8)
keeping in mind that for 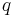 and
and 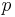 being constants, we have
being constants, we have
-
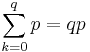 .
.(9)
It can then be verified that (8) and (2) give the same result for 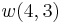 ,
, 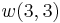 ,
,  , etc.
, etc.
Interdisciplinary applications
Viewed as a pure probability distribution, the Bose-Einstein distribution has found application in other fields:
- In recent years, Bose Einstein statistics have also been used as a method for term weighting in information retrieval. The method is one of a collection of DFR ("Divergence From Randomness") models, the basic notion being that Bose Einstein statistics may be a useful indicator in cases where a particular term and a particular document have a significant relationship that would not have occurred purely by chance. Source code for implementing this model is available from the Terrier project at the University of Glasgow.
-
Main article: Bose–Einstein condensation (network theory)The evolution of many complex systems, including the World Wide Web, business, and citation networks, is encoded in the dynamic web describing the interactions between the system’s constituents. Despite their irreversible and nonequilibrium nature these networks follow Bose statistics and can undergo Bose–Einstein condensation. Addressing the dynamical properties of these nonequilibrium systems within the framework of equilibrium quantum gases predicts that the “first-mover-advantage,” “fit-get-rich(FGR),” and “winner-takes-all” phenomena observed in competitive systems are thermodynamically distinct phases of the underlying evolving networks.[1]
See also
- Bose–Einstein correlations
- Boson
- Higgs boson
- Maxwell–Boltzmann statistics
- Fermi–Dirac statistics
- Parastatistics
- Planck's law of black body radiation
Notes
- ^ Bianconi, G.; Barabási, A.-L. (2001). "Bose–Einstein Condensation in Complex Networks." Phys. Rev. Lett. 86: 5632–35.
References
- Annett, James F. (2004). Superconductivity, Superfluids and Condensates. New York: Oxford University Press. ISBN 0198507550.
- Carter, Ashley H. (2001). Classical and Statistical Thermodynamics. Upper Saddle River, NJ: Prentice Hall. ISBN 0137792085.
- Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Upper Saddle River, NJ: Pearson, Prentice Hall. ISBN 0131911759.
|
||||||||||||||||||||||||||