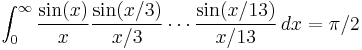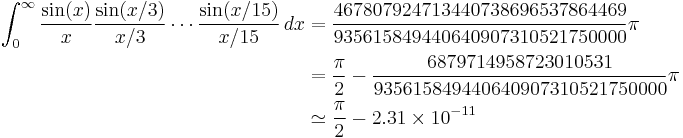Borwein integral

In mathematics, a Borwein integral is an integral studied by Borwein & Borwein (2001) involving products of sinc(ax), where the sinc function is given by sinc(x) = sin(x)/x. These integrals are notorious for exhibiting apparent patterns that eventually break down. An example they give is

\begin{align} & \int_0^\infty \frac{\sin(x)}{x} \, dx=\pi/2 \\[10pt] & \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3} \, dx = \pi/2 \\[10pt] & \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\frac{\sin(x/5)}{x/5} \, dx = \pi/2 \end{align}

This pattern continues up to

\int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/13)}{x/13} \, dx = \pi/2

However at the next step the obvious pattern fails:

\begin{align} \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/15)}{x/15} \, dx &= \frac{467807924713440738696537864469}{935615849440640907310521750000}\pi \\ &= \frac{\pi}{2} - \frac{6879714958723010531}{935615849440640907310521750000}\pi \\ &\simeq \frac{\pi}{2} - 2.31\times 10^{-11} \end{align}

In general similar integrals have value π/2 whenever the numbers 3, 5, ... are replaced by positive real numbers such that the sum of their reciprocals is less than 1. In the example above, 1/3 + 1/5 + ... + 1/13 < 1, but 1/3 + 1/5 + ... + 1/15 > 1.

References