Cobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes from the French word bord for boundary. The boundary of an 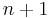 -dimensional manifold
-dimensional manifold  is an
is an  -dimensional manifold
-dimensional manifold 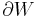 that is closed, i.e., with empty boundary. In general, a closed manifold need not be a boundary: cobordism theory is the study of the difference between all closed manifolds and those that are boundaries. The theory was originally developed for smooth (i.e., differentiable) manifolds, but there are now also versions for piecewise-linear and topological manifolds.
that is closed, i.e., with empty boundary. In general, a closed manifold need not be a boundary: cobordism theory is the study of the difference between all closed manifolds and those that are boundaries. The theory was originally developed for smooth (i.e., differentiable) manifolds, but there are now also versions for piecewise-linear and topological manifolds.
A cobordism is a manifold  with boundary whose boundary is partitioned in two,
with boundary whose boundary is partitioned in two, 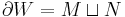 .
.
Cobordisms are studied both for the equivalence relation that they generate, and as objects in their own right. Cobordism is a much coarser equivalence relation than diffeomorphism or homeomorphism of manifolds, and is significantly easier to study and compute. It is not possible to classify manifolds up to diffeomorphism or homeomorphism in dimensions 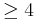 – because the word problem for groups cannot be solved - but it is possible to classify manifolds up to cobordism. Cobordisms are central objects of study in geometric topology and algebraic topology. In geometric topology, cobordisms are intimately connected with Morse theory, and h-cobordisms are fundamental in the study of high dimensional manifolds, namely surgery theory. In algebraic topology, cobordism theories are fundamental extraordinary cohomology theories, and categories of cobordisms are the domains of topological quantum field theories.
– because the word problem for groups cannot be solved - but it is possible to classify manifolds up to cobordism. Cobordisms are central objects of study in geometric topology and algebraic topology. In geometric topology, cobordisms are intimately connected with Morse theory, and h-cobordisms are fundamental in the study of high dimensional manifolds, namely surgery theory. In algebraic topology, cobordism theories are fundamental extraordinary cohomology theories, and categories of cobordisms are the domains of topological quantum field theories.
Contents |
Definition
More formally, an 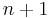 -dimensional cobordism is a quintuple
-dimensional cobordism is a quintuple 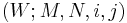 consisting of an
consisting of an 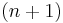 -manifold with boundary
-manifold with boundary 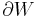 , closed
, closed  -manifolds
-manifolds 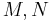 and embeddings
and embeddings 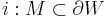 ,
,  with disjoint images such that
with disjoint images such that
The terminology is usually abbreviated to 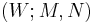 .[1]
.[1]
Every closed manifold  is the boundary of the non-compact manifold
is the boundary of the non-compact manifold 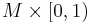 . So for the purposes of cobordism theory only compact manifolds are considered.
. So for the purposes of cobordism theory only compact manifolds are considered.
The above is the most basic (unoriented) form of the definition. In most practical situations, the manifolds in question are oriented, or carry some additional G-structure. One defines "oriented cobordism" and "cobordism with G-structure", but there are various technicalities. In each particular case, cobordism is an equivalence relation on manifolds. A basic question is to determine the equivalence classes for this relationship, called the cobordism classes of manifolds. Under favourable technical conditions these form a graded ring called the cobordism ring 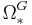 , with grading by dimension, addition by disjoint union and multiplication by cartesian product. The cobordism groups
, with grading by dimension, addition by disjoint union and multiplication by cartesian product. The cobordism groups 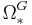 are the coefficient groups of a generalised homology theory.
are the coefficient groups of a generalised homology theory.
Main ideas
This section sets out some of the mathematical background to cobordism.
Manifolds with boundary
An n+1-dimensional manifold with boundary is a topological space that is a union of the interior and the boundary: each point in the interior has a neighbourhood homeomorphic to the Euclidean n+1-dimensional space 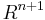 and each point in the boundary has a neighbourhood homeomorphic to the Euclidean n+1-dimensional half-space
and each point in the boundary has a neighbourhood homeomorphic to the Euclidean n+1-dimensional half-space 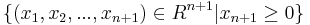 . In both cases, the point corresponds to the origin
. In both cases, the point corresponds to the origin 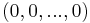 .
.
Additional geometric structure
In most applications, the manifold  comes with additional geometric structure, such as a map to some reference space, or additional bundle data. One then wants the surgery process to endow
comes with additional geometric structure, such as a map to some reference space, or additional bundle data. One then wants the surgery process to endow 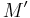 with the same kind of additional structure. For instance, a standard tool in surgery theory is surgery on normal maps: such a process changes a normal map to another normal map within the same bordism class.
with the same kind of additional structure. For instance, a standard tool in surgery theory is surgery on normal maps: such a process changes a normal map to another normal map within the same bordism class.
The surgery construction of cobordisms
Recall that in general, if 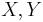 are manifolds with boundary, then the boundary of the product manifold is
are manifolds with boundary, then the boundary of the product manifold is 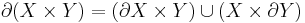 .
.
Now, given a manifold 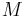 of dimension
of dimension 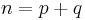 and an embedding
and an embedding 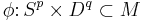 , define the
, define the  -manifold
-manifold
obtained by surgery, via cutting out the interior of 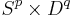 and gluing in
and gluing in 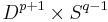 along their boundary
along their boundary 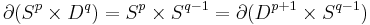 . The trace of the surgery
. The trace of the surgery
defines an elementary cobordism 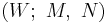 . Note that
. Note that  is obtained from
is obtained from  by surgery on
by surgery on 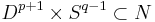 . This is called reversing the surgery.
. This is called reversing the surgery.
Every cobordism is a union of elementary cobordisms, by the work of Morse, Thom and Milnor.
Examples
1. The unit line
The unit line ![[0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/ccfcd347d0bf65dc77afe01a3306a96b.png) is a 1-dimensional cobordism between the 0-dimensional manifolds
is a 1-dimensional cobordism between the 0-dimensional manifolds 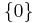 ,
, 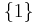 , and more generally for any closed manifold
, and more generally for any closed manifold  there is defined a cobordism
there is defined a cobordism ![M \times ([0,1];\{0\},\{1\})](/2012-wikipedia_en_all_nopic_01_2012/I/4b9541bc326e9c619afb5fd88ac81962.png) from
from 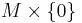 to
to 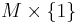 .
.
2. Pair of pants
If M consists of a circle, and N of two circles, M and N together make up the boundary of a pair of pants W (see the figure at right). Thus the pair of pants is a cobordism between M and N.
More generally, this picture shows that for any two  -dimensional manifolds
-dimensional manifolds 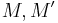 , the disjoint union
, the disjoint union  and connected sum
and connected sum 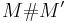 are cobordant, as the first corresponds to
are cobordant, as the first corresponds to 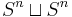 and the latter to
and the latter to 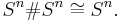 The connected sum
The connected sum 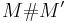 is obtained from the disjoint union
is obtained from the disjoint union  by surgery on an embedding
by surgery on an embedding 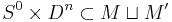 , and the cobordism is the trace of the surgery.
, and the cobordism is the trace of the surgery.
3. Surgery on the Circle
As per the above definition, a surgery on the circle consists of cutting out a copy of 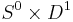 and glueing in
and glueing in 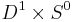 . The pictures in Fig. 1 show that the result of doing this is either (i)
. The pictures in Fig. 1 show that the result of doing this is either (i) 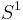 again, or (ii) two copies of
again, or (ii) two copies of 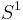 .
.
4. Surgery on the 2-Sphere
In this case there are more possibilities, since we can start by cutting out either 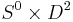 or
or 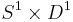 .
.
- (a)
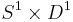 : If we remove a cylinder from the 2-sphere, we are left with two disks. We have to glue back in
: If we remove a cylinder from the 2-sphere, we are left with two disks. We have to glue back in 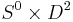 - that is, two disks - and it's clear that the result of doing so is to give us two disjoint spheres. (Fig. 2a)
- that is, two disks - and it's clear that the result of doing so is to give us two disjoint spheres. (Fig. 2a)
- (b)
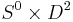 : Having cut out two disks
: Having cut out two disks 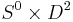 , we glue back in the cylinder
, we glue back in the cylinder 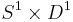 . Interestingly, there are two possible outcomes, depending on whether our glueing maps have the same or opposite orientation on the two boundary circles. If the orientations are the same (Fig. 2b), the resulting manifold is the torus
. Interestingly, there are two possible outcomes, depending on whether our glueing maps have the same or opposite orientation on the two boundary circles. If the orientations are the same (Fig. 2b), the resulting manifold is the torus 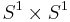 , but if they are different, we obtain the Klein Bottle (Fig. 2c).
, but if they are different, we obtain the Klein Bottle (Fig. 2c).
5. Morse functions
Suppose that  is a Morse function on an
is a Morse function on an 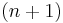 -dimensional manifold, and suppose that
-dimensional manifold, and suppose that  is a critical value with exactly one critical point in its preimage. If the index of this critical point is
is a critical value with exactly one critical point in its preimage. If the index of this critical point is 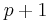 , then the level-set
, then the level-set 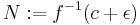 is obtained from
is obtained from 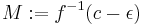 by a
by a  -surgery. The inverse image
-surgery. The inverse image ![W:=f^{-1}([c-\epsilon,c%2B\epsilon])](/2012-wikipedia_en_all_nopic_01_2012/I/2fd7508229e557e051b68724db1f8eba.png) defines a cobordism
defines a cobordism 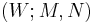 that can be identified with the trace of this surgery.
that can be identified with the trace of this surgery.
Manifolds that are not boundaries
The 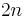 -dimensional real projective space RP2n is the simplest example of a (compact) closed manifold that is not the boundary of a manifold: the Euler characteristic of a boundary must be even, but the Euler characteristic of RP2n is 1. More generally, any product of even-dimensional real projective spaces is not a boundary.
-dimensional real projective space RP2n is the simplest example of a (compact) closed manifold that is not the boundary of a manifold: the Euler characteristic of a boundary must be even, but the Euler characteristic of RP2n is 1. More generally, any product of even-dimensional real projective spaces is not a boundary.
History
Cobordism had its roots in the (failed) attempt by Henri Poincaré in 1895 to define homology purely in terms of manifolds (Dieudonné 1989, p. 289). Poincaré simultaneously defined both homology and cobordism, which are not the same, in general. See Cobordism as an extraordinary cohomology theory for the relationship between bordism and homology.
Bordism was explicitly introduced by Lev Pontryagin in geometric work on manifolds. It came to prominence when René Thom showed that cobordism groups could be computed by means of homotopy theory, via the Thom complex construction. Cobordism theory became part of the apparatus of extraordinary cohomology theory, alongside K-theory. It performed an important role, historically speaking, in developments in topology in the 1950s and early 1960s, in particular in the Hirzebruch-Riemann-Roch theorem, and in the first proofs of the Atiyah-Singer index theorem.
In the 1980s the category with compact manifolds as objects and cobordisms between these as morphisms played a basic role in the Atiyah-Segal axioms for topological quantum field theory, which is an important part of quantum topology.
Context
Cobordisms are objects of study in their own right, apart from cobordism classes. Categorically, one can also think of a cobordism 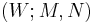 as a map from M to N, and thus define categories of cobordisms. A cobordism is a kind of cospan:[2] M → W ← N.
as a map from M to N, and thus define categories of cobordisms. A cobordism is a kind of cospan:[2] M → W ← N.
Terminology
An n-manifold M is called null-cobordant if there is a cobordism between M and the empty manifold; in other words, if M is the entire boundary of some (n+1)-manifold. Equivalently, its cobordism class is trivial.
For example:
- The circle (and more generally, n-sphere) are null-cobordant since they bound an (n+1)-disk.
- Every orientable surface is null-cobordant, because it is the boundary of a handlebody.
Null-cobordisms with additional structure are called fillings. "Bordism" and "cobordism" are sometimes used interchangeably; others distinguish them. When one wishes to distinguish the study of cobordism classes from the study of cobordisms as objects in their own right, one calls the equivalence question "bordism of manifolds", and the study of cobordisms as objects "cobordisms of manifolds".
The term "bordism" comes from French bord, meaning boundary. Hence bordism is the study of boundaries. "Cobordism" means "jointly bound", so M and N are cobordant if they jointly bound a manifold, i.e., if their disjoint union is a boundary. Further, cobordism groups form an extraordinary cohomology theory, hence the co-.
Geometry, and the connection with Morse theory and handlebodies
Given a cobordism 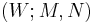 there exists a smooth function
there exists a smooth function ![f�: W \to [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/5b146c3b55fd1799e36bcaac517f974d.png) such that
such that 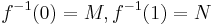 . By general position, one can assume
. By general position, one can assume  is Morse and such that all critical points occur in the interior of
is Morse and such that all critical points occur in the interior of  . In this setting
. In this setting  is called a Morse function on a cobordism. The cobordism
is called a Morse function on a cobordism. The cobordism 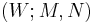 is a union of the traces of a sequence of surgeries on
is a union of the traces of a sequence of surgeries on  , one for each critical point of
, one for each critical point of  . The manifold
. The manifold  is obtained from
is obtained from ![M \times [0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/8133e1a3347bba0eb3f5fa606d7e548f.png) by attaching one handle for each critical point of
by attaching one handle for each critical point of 
The Morse/Smale theorem states that for a Morse function on a cobordism, the flowlines of 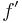 give rise to a handle presentation of the triple
give rise to a handle presentation of the triple 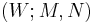 . Conversely, given a handle decomposition of a cobordism, it comes from a suitable Morse function. In a suitably normalized setting this process gives a correspondence between handle decompositions and Morse functions on a cobordism.
. Conversely, given a handle decomposition of a cobordism, it comes from a suitable Morse function. In a suitably normalized setting this process gives a correspondence between handle decompositions and Morse functions on a cobordism.
Development
This section covers cobordism of manifolds with different types of structures, and algebraic topological calculations concerned with these.
Cobordism classes
The general bordism problem is to calculate the cobordism classes of manifolds subject to various conditions.
 -cobordism
-cobordism
When there is additional structure, the notion of cobordism must be formulated more precisely: a  -structure on
-structure on  restricts to a
restricts to a  -structure on
-structure on  and
and  . The basic examples are
. The basic examples are 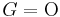 for unoriented cobordism,
for unoriented cobordism, 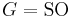 for oriented cobordism, and
for oriented cobordism, and 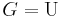 for complex cobordism using stably complex manifolds. Many more are detailed by Stong.[3]
for complex cobordism using stably complex manifolds. Many more are detailed by Stong.[3]
Unoriented cobordism
The cobordism class ![[M] \in \Omega_n^{\text{O}}](/2012-wikipedia_en_all_nopic_01_2012/I/993afe03c9843420a484ba5addb686b9.png) of a closed
of a closed  -dimensional manifold
-dimensional manifold  is determined by the Stiefel-Whitney characteristic numbers, which depend on the stable isomorphism class of the tangent bundle. Thus if
is determined by the Stiefel-Whitney characteristic numbers, which depend on the stable isomorphism class of the tangent bundle. Thus if  has a stably trivial tangent bundle then
has a stably trivial tangent bundle then ![[M]=0 \in \Omega_n^{\text{O}}](/2012-wikipedia_en_all_nopic_01_2012/I/5b8b2e3430df86b4a1cc38b464f9564e.png) . Every closed manifold
. Every closed manifold  is such that
is such that 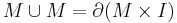 , so
, so 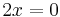 for every
for every 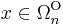 . In 1954 René Thom computed
. In 1954 René Thom computed
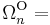 Z
Z![_2[x_i \vert i \geq 1, i \neq 2^j -1 ]](/2012-wikipedia_en_all_nopic_01_2012/I/af1a419ea5e12233947000add9126c41.png)
with one generator  in each dimension
in each dimension 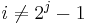 . For even
. For even  is possible to choose
is possible to choose ![x_i=[\mathbb{R}\mathbb{P}^i]](/2012-wikipedia_en_all_nopic_01_2012/I/dc797efa1c7bc042a0fd3d61e36f999b.png) , the cobordism class of the
, the cobordism class of the  -dimensional real projective space.
-dimensional real projective space.
The low-dimensional unoriented cobordism groups are
The mod2 Euler characteristic 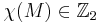 of an unoriented
of an unoriented 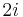 -dimensional manifold
-dimensional manifold  is an unoriented cobordism invariant. For example, for any
is an unoriented cobordism invariant. For example, for any 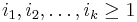
The mod2 Euler characteristic map 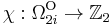 is onto for all
is onto for all 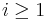 , and an isomorphism for
, and an isomorphism for 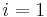 .
.
Oriented cobordism
Assume all manifolds are oriented. Then an oriented cobordism is a manifold W whose boundary (with the induced orientations) is 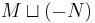 , where
, where 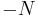 denotes
denotes  with the reversed orientation.
with the reversed orientation.
Why the reversed orientation? Firstly, because as oriented manifolds, the boundary of the cylinder 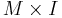 is
is 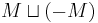 : both ends have opposite orientations (this is most familiar for the interval:
: both ends have opposite orientations (this is most familiar for the interval: 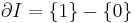 ). It is also the correct definition in the sense of extraordinary cohomology theory. For an oriented closed manifold
). It is also the correct definition in the sense of extraordinary cohomology theory. For an oriented closed manifold  it is not in general the case that
it is not in general the case that 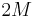 is an oriented boundary, and the cobordism class
is an oriented boundary, and the cobordism class ![[M] \in \Omega_*^{\text{SO}}](/2012-wikipedia_en_all_nopic_01_2012/I/242343beb50f845223f43a051ba5e0ec.png) could have infinite torsion, i.e., such that
could have infinite torsion, i.e., such that ![k[M] \neq 0](/2012-wikipedia_en_all_nopic_01_2012/I/0909ca86564d6bf8ca0cf924605e7e27.png) for every non-zero integer
for every non-zero integer 
The oriented cobordism groups are given modulo torsion by
![\Omega_*^{\text{SO}}\otimes \mathbb{Q}~=~\mathbb{Q}[y_{4i}|i \geq 1]](/2012-wikipedia_en_all_nopic_01_2012/I/4a5bc48b37efe42adcb953e8321cce0b.png) ,
,
the polynomial algebra generated by the oriented cobordism classes ![y_{4i}=[\mathbb{CP}^{2i}] \in \Omega_{4i}^{\text{SO}}](/2012-wikipedia_en_all_nopic_01_2012/I/568ef04d0e7614b6de3ab52d6e4043eb.png) of the complex projective spaces (Thom, 1952) The oriented cobordism group
of the complex projective spaces (Thom, 1952) The oriented cobordism group 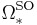 is determined by the Stiefel-Whitney and Pontrjagin characteristic numbers (Wall, 1960). Two oriented manifolds are oriented cobordism if and only if their Stiefel-Whitney and Pontrjagin numbers are the same.
is determined by the Stiefel-Whitney and Pontrjagin characteristic numbers (Wall, 1960). Two oriented manifolds are oriented cobordism if and only if their Stiefel-Whitney and Pontrjagin numbers are the same.
The low-dimensional oriented cobordism groups are
The signature of an oriented 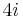 -dimensional manifold
-dimensional manifold 
is an oriented cobordism invariant, which is expressed in terms of the Pontrjagin numbers by the Hirzebruch signature theorem.
For example, for any 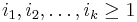
The signature map 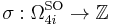 is onto for all
is onto for all 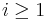 , and an isomorphism for
, and an isomorphism for 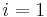 .
.
Cobordism as an extraordinary cohomology theory
Every vector bundle theory (real, complex etc.) has a extraordinary cohomology theory called K-theory. Similarly, every cobordism theory 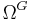 has an extraordinary cohomology theory, with homology ("bordism") groups
has an extraordinary cohomology theory, with homology ("bordism") groups 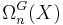 and cohomology ("cobordism") groups
and cohomology ("cobordism") groups 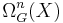 for any space
for any space  . The generalized homology groups
. The generalized homology groups 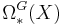 are covariant in
are covariant in  , and the generalized cohomology groups
, and the generalized cohomology groups 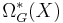 are contravariant in
are contravariant in  . The cobordism groups defined above are, from this point of view, the homology groups of a point:
. The cobordism groups defined above are, from this point of view, the homology groups of a point: 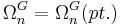 . Then
. Then 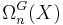 is the group of bordism classes of pairs
is the group of bordism classes of pairs 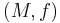 with
with  a closed
a closed  -dimensional manifold
-dimensional manifold  (with G-structure) and
(with G-structure) and 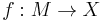 a map. Such pairs
a map. Such pairs 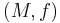 ,
, 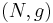 are bordant if there exists a G-cobordism
are bordant if there exists a G-cobordism 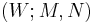 with a map
with a map 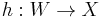 , which restricts to
, which restricts to  on
on  , and to
, and to  on
on  .
.
An  -dimensional manifold
-dimensional manifold  has a fundamental homology class
has a fundamental homology class ![[M] \in H_n(M)](/2012-wikipedia_en_all_nopic_01_2012/I/7c20db777f4c05b172933122c0fa1662.png) (with coefficients in
(with coefficients in 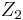 in general, and in
in general, and in 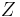 in the oriented case), defining a natural transformation
in the oriented case), defining a natural transformation
which is far from being an isomorphism in general.
The bordism and cobordism theories of a space satisfy the Eilenberg-Steenrod axioms apart from the dimension axiom. This does not mean that the groups 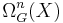 can be effectively computed once one knows the cobordism theory of a point and the homology of the space X, though the Atiyah-Hirzebruch spectral sequence gives a starting point for calculations. The computation is only easy if the particular cobordism theory reduces to a product of ordinary homology theories, in which case the bordism groups are the ordinary homology groups
can be effectively computed once one knows the cobordism theory of a point and the homology of the space X, though the Atiyah-Hirzebruch spectral sequence gives a starting point for calculations. The computation is only easy if the particular cobordism theory reduces to a product of ordinary homology theories, in which case the bordism groups are the ordinary homology groups
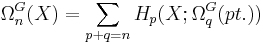 .
.
This is true for unoriented cobordism. Other cobordism theories do not reduce to ordinary homology in this way, notably framed cobordism, oriented cobordism and complex cobordism. The last-named theory in particular is much used by algebraic topologists as a computational tool (e.g., for the homotopy groups of spheres). [4]
Cobordism theories are represented by Thom spectra  : given a group G, the Thom spectrum is composed from the Thom spaces
: given a group G, the Thom spectrum is composed from the Thom spaces  of the standard vector bundles over the classifying spaces
of the standard vector bundles over the classifying spaces  . Note that even for similar groups, Thom spectra can be very different:
. Note that even for similar groups, Thom spectra can be very different: 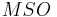 and
and 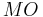 are very different, reflecting the difference between oriented and unoriented cobordism.
are very different, reflecting the difference between oriented and unoriented cobordism.
From the point of view of spectra, unoriented cobordism is a product of Eilenberg-MacLane spectra – 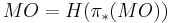 – while oriented cobordism is a product of Eilenberg-MacLane spectra rationally, and at 2, but not at odd primes: the oriented cobordism spectrum
– while oriented cobordism is a product of Eilenberg-MacLane spectra rationally, and at 2, but not at odd primes: the oriented cobordism spectrum 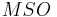 is rather more complicated than
is rather more complicated than 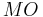 .
.
Categories of cobordisms
Cobordisms form a category where the objects are closed manifolds and the morphisms are cobordisms. Composition is given by gluing together cobordisms end-to-end: the composition of 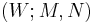 and
and 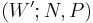 is defined by gluing the right end of the first to the left end of the second, yielding
is defined by gluing the right end of the first to the left end of the second, yielding 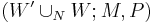 .
.
A topological quantum field theory is a monoidal functor from a category of cobordisms to a category of vector spaces. That is, it is a functor whose value on a disjoint union of manifolds is equivalent to the tensor product of its values on each of the constituent manifolds.
In low dimensions, the bordism question is trivial, but the category of cobordism is still interesting. For instance, the disk bounding the circle corresponds to a null-ary operation, while the cylinder corresponds to a 1-ary operation and the pair of pants to a binary operation.
Cobordism of piecewise linear and topological manifolds
Originally, cobordism was introduced for differentiable manifolds. The theory works also for PL and topological manifolds, with bordism groups 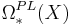 ,
, 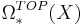 , which are generalized homology groups. The cobordism groups of PL and topological manifolds are harder to compute.
, which are generalized homology groups. The cobordism groups of PL and topological manifolds are harder to compute.
See also
Notes
- ^ The notation "
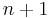 -dimensional" is to clarify the dimension of all manifolds in question, otherwise it is unclear whether a "5-dimensional cobordism" refers to a 5-dimensional cobordism between 4-dimensional manifolds or a 6-dimensional cobordism between 5-dimensional manifolds.
-dimensional" is to clarify the dimension of all manifolds in question, otherwise it is unclear whether a "5-dimensional cobordism" refers to a 5-dimensional cobordism between 4-dimensional manifolds or a 6-dimensional cobordism between 5-dimensional manifolds. - ^ While every cobordism is a cospan, the category of cobordisms is not a "cospan category": it is not the category of all cospans in "the category of manifolds with inclusions on the boundary", but rather a subcategory thereof, as the requirement that M and N form a partition of the boundary of W is a global constraint.
- ^ Stong, Robert E. (1968). Notes on cobordism theory. Princeton University Press.
- ^ Ravenel, D.C. (April 1986). Complex cobordism and stable homotopy groups of spheres. Academic Press. ISBN 0125834306
References
- J. F. Adams, Stable homotopy and generalised homology, Univ. Chicago Press (1974).
- Anosov, D. V.; Voitsekhovskii, M. I. (2001), "bordism", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=b/b017030
- M. F. Atiyah, Bordism and cobordism Proc. Camb. Phil. Soc. 57, pp. 200–208 (1961).
- Dieudonné, Jean Alexandre (1989). A history of algebraic and differential topology, 1900-1960. Boston: Birkhäuser. ISBN 978 0 81763388 2
- Kosinski, A. (October 19, 2007). Differential Manifolds. Dover Publications
- Madsen, Ib; Milgram, R. James (1979). The classifying spaces for surgery and cobordism of manifolds. Princeton, New Jersey: Princeton University Press. ISBN 978 0 69108226 4
- J. Milnor (1962). "A survey of cobordism theory". L'Enseignement Mathématique. Revue Internationale. IIe Série 8: 16–23. ISSN 0013-8584.
- S. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Izv. Akad. Nauk SSSR Ser. Mat. 31 (1967), 855–951.
- L. Pontryagin, Smooth manifolds and their applications in homotopy theory American Mathematical Society Translations, Ser. 2, Vol. 11, pp. 1–114 (1959).
- D. Quillen, On the formal group laws of unoriented and complex cobordism theory Bull. Amer. Math. Soc, 75 (1969) pp. 1293–1298.
- D. C. Ravenel, Complex cobordism and stable homotopy groups of spheres, Acad. Press (1986).
- Yu. B. Rudyak (2001), "Cobordism", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c022780
- Yu. B. Rudyak, On Thom spectra, orientability, and (co)bordism, Springer (2008).
- R. E. Stong, Notes on cobordism theory, Princeton Univ. Press (1968).
- Taimanov, I. A. (2007). Topological library. Part 1: cobordisms and their applications. Series on Knots and Everything. 39. S. Novikov (ed.). World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ. ISBN 978-981-270-559-4; 981-270-559-7.
- R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, 17-86 (1954).
- C. T. C. Wall (1960). "Determination of the cobordism ring". Annals of Mathematics. Second Series (The Annals of Mathematics, Vol. 72, No. 2) 72 (2): 292–311. doi:10.2307/1970136. ISSN 0003-486X. JSTOR 1970136.
External links
- Bordism on the Manifold Atlas.
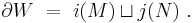
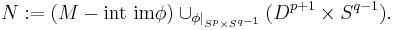
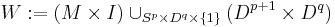
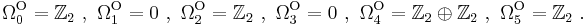
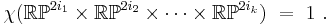
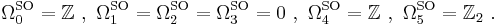
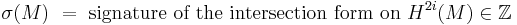
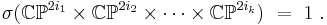
![\Omega^G_n(X) \to H_n(X);(M,f) \to f_*[M]~,](/2012-wikipedia_en_all_nopic_01_2012/I/e3a884c0823b691d2d9936e2adc3dc7f.png)