Bootstrapping (statistics)

In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates (Efron and Tibshirani 1993). This technique allows estimation of the sample distribution of almost any statistic using only very simple methods (Varian 2005).[1] Generally, it falls in the broader class of resampling methods.

Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples of the observed dataset (and of equal size to the observed dataset), each of which is obtained by random sampling with replacement from the original dataset.

It may also be used for constructing hypothesis tests. It is often used as an alternative to inference based on parametric assumptions when those assumptions are in doubt, or where parametric inference is impossible or requires very complicated formulas for the calculation of standard errors.

Contents

Advantages

A great advantage of bootstrap is its simplicity. It is straightforward to derive estimates of standard errors and confidence intervals for complex estimators of complex parameters of the distribution, such as percentile points, proportions, odds ratio, and correlation coefficients. Moreover, it is an appropriate way to control and check the stability of the results.

Disadvantages

Although bootstrapping is (under some conditions) asymptotically consistent, it does not provide general finite-sample guarantees. Furthermore, it has a tendency to be overly optimistic. The apparent simplicity may conceal the fact that important assumptions are being made when undertaking the bootstrap analysis (e.g. independence of samples) where these would be more formally stated in other approaches.

Informal description

The basic idea of bootstrapping is that the sample we have collected is often the best guess we have as to the shape of the population from which the sample was taken. For instance, a sample of observations with two peaks in its histogram would not be well approximated by a Gaussian or normal bell curve, which has only one peak. Therefore, instead of assuming a mathematical shape (like the normal curve or some other) for the population, we instead use the shape of the sample.

As an example, assume we are interested in the average (or mean) height of people worldwide. We cannot measure all the people in the global population, so instead we sample only a tiny part of it, and measure that. Assume the sample is of size N; that is, we measure the heights of N individuals. From that single sample, only one value of the mean can be obtained. In order to reason about the population, we need some sense of the variability of the mean that we have computed.

To use the simplest bootstrap technique, we take our original data set of N heights, and, using a computer, make a new sample (called a bootstrap sample) that is also of size N. This new sample is taken from the original using sampling with replacement so it is not identical with the original "real" sample. We repeat this a lot (maybe 1000 or 10,000 times), and for each of these bootstrap samples we compute its mean (each of these are called bootstrap estimates). We now have a histogram of bootstrap means. This provides an estimate of the shape of the distribution of the mean from which we can answer questions about how much the mean varies. (The method here, described for the mean, can be applied to almost any other statistic or estimator.)

The key principle of the bootstrap is to provide a way to simulate repeated observations from an unknown population using the obtained sample as a basis.

Situations where "Bootstrapping procedures" are useful

Adèr et al.(2008) recommend the bootstrap procedure for the following situations:

  • When the theoretical distribution of a statistic of interest is complicated or unknown. Since the bootstrapping procedure is distribution-independent it provides an indirect method to assess the properties of the distribution underlying the sample and the parameters of interest that are derived from this distribution.
  • When the sample size is insufficient for straightforward statistical inference. If the underlying distribution is well-known, bootstrapping provides a way to account for the distortions caused by the specific sample that may not be fully representative of the population.
  • When power calculations have to be performed, and a small pilot sample is available. Most power and sample size calculations are heavily dependent on the standard deviation of the statistic of interest. If the estimate used is incorrect, the required sample size will also be wrong. One method to get an impression of the variation of the statistic is to use a small pilot sample and perform bootstrapping on it to get impression of the variance.

Recommendation

The number of bootstrap samples recommended in literature has increased as available computing power has increased. If the results really matter, as many samples as is reasonable given available computing power and time should be used. Increasing the number of samples cannot increase the amount of information in the original data, it can only reduce the effects of random sampling errors which can arise from a bootstrap procedure itself.

Types of bootstrap scheme

In univariate problems, it is usually acceptable to resample the individual observations with replacement ("case resampling" below). In small samples, a parametric bootstrap approach might be preferred. For other problems, a smooth bootstrap will likely be preferred.

For regression problems, various other alternatives are available.

Case resampling

Bootstrap is generally useful for estimating the distribution of a statistic (e.g. mean, variance) without using normal theory (e.g. z-statistic, t-statistic). Bootstrap comes in handy when there is no analytical form or normal theory to help estimate the distribution of the statistics of interest, since bootstrap method can apply to most random quantities, e.g., the ratio of variance and mean. There are at least two ways of performing case resampling.

  1. The Monte Carlo algorithm for case resampling is quite simple. First, we resample the data with replacement, and the size of the resample must be equal to the size of the original data set. Then the statistic of interest is computed from the resample from the first step. We repeat this routine many times to get a more precise estimate of the Bootstrap distribution of the statistic.
  2. The 'exact' version for case resampling is similar, but we exhaustively enumerate every possible resample of the data set. This can be computationally expensive as there are a total of 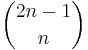\binom {2n-1}n different resamples, where n is the size of the data set.

Estimating the distribution of sample mean

Consider a coin-flipping experiment. We flip the coin and record whether it lands heads or tails. (Assume for simplicity that there are only two outcomes) Let X = x1, x2, …, x10 be 10 observations from the experiment. xi = 1 if the i th flip lands heads, and 0 otherwise. From normal theory, we can use t-statistic to estimate the distribution of the sample mean, 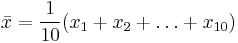\bar{x} = \frac{1}{10} (x_1 %2B x_2 %2B \ldots %2B x_{10}).

Instead, we use bootstrap, specifically case resampling, to derive the distribution of 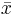\bar{x}. We first resample the data to obtain a bootstrap resample. An example of the first resample might look like this X1* = x2, x1, x10, x10, x3, x4, x6, x7, x1, x9. Note that there are some duplicates since a bootstrap resample comes from sampling with replacement from the data. Note also that the number of data points in a bootstrap resample is equal to the number of data points in our original observations. Then we compute the mean of this resample and obtain the first bootstrap mean: μ1*. We repeat this process to obtain the second resample X2* and compute the second bootstrap mean μ2*. If we repeat this 100 times, then we have μ1*, μ2*, …, μ100*. This represents an empirical bootstrap distribution of sample mean. From this empirical distribution, one can derive a bootstrap confidence interval for the purpose of hypothesis testing.

Regression

In regression problems, case resampling refers to the simple scheme of resampling individual cases - often rows of a data set. For regression problems, so long as the data set is fairly large, this simple scheme is often acceptable. However, the method is open to criticism.

In regression problems, the explanatory variables are often fixed, or at least observed with more control than the response variable. Also, the range of the explanatory variables defines the information available from them. Therefore, to resample cases means that each bootstrap sample will lose some information. As such, alternative bootstrap procedures should be considered.

Smooth bootstrap

Under this scheme, a small amount of (usually normally distributed) zero-centered random noise is added on to each resampled observation. This is equivalent to sampling from a kernel density estimate of the data.

Parametric bootstrap

In this case a parametric model is fitted to the data, often by maximum likelihood, and samples of random numbers are drawn from this fitted model. Usually the sample drawn has the same sample size as the original data. Then the quantity, or estimate, of interest is calculated from these data. This sampling process is repeated many times as for other bootstrap methods. The use of a parametric model at the sampling stage of the bootstrap methodology leads to procedures which are different from those obtained by applying basic statistical theory to inference for the same model.

Resampling residuals

Another approach to bootstrapping in regression problems is to resample residuals. The method proceeds as follows.

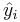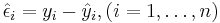  1. Fit the model and retain the fitted values \hat y_i and the residuals \hat{\epsilon}_i = y_i - \hat{y}_i, (i = 1,\dots, n).
  2. For each pair, (xi, yi), in which xi is the (possibly multivariate) explanatory variable, add a randomly resampled residual, 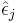\hat{\epsilon}_j, to the response variable yi. In other words create synthetic response variables 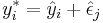y^*_i = \hat{y}_i %2B \hat{\epsilon}_j where j is selected randomly from the list (1, …, n) for every i.
  3. Refit the model using the fictitious response variables y*i, and retain the quantities of interest (often the parameters, 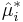\hat\mu^*_i, estimated from the synthetic y*i).
  4. Repeat steps 2 and 3 a statistically significant number of times.

This scheme has the advantage that it retains the information in the explanatory variables. However, a question arises as to which residuals to resample. Raw residuals are one option; another is studentized residuals (in linear regression). Whilst there are arguments in favour of using studentized residuals; in practice, it often makes little difference and it is easy to run both schemes and compare the results against each other.

Gaussian process regression bootstrap

When data are temporally correlated, straightforward bootstrapping destroys the inherent correlations. This method uses Gaussian process regression to fit a probabilistic model from which replicates may then be drawn. Gaussian processes are methods from Bayesian non-parametric statistics but are here used to construct a parametric bootstrap approach, which implicitly allows the time-dependence of the data to be taken into account.

Wild bootstrap

Each residual is randomly multiplied by a random variable with mean 0 and variance 1. This method assumes that the 'true' residual distribution is symmetric and can offer advantages over simple residual sampling for smaller sample sizes.[2]

Moving block bootstrap

In the moving block bootstrap, n-b+1 overlapping blocks of length b will be created in the following way: Observation 1 to b will be block 1, observation 2 to b+1 will be block 2 etc. Then from these n-b+1 blocks, n/b blocks will be drawn at random with replacement. Then aligning these n/b blocks in the order they were picked, will give the bootstrap observations. This bootstrap works with dependent data, however, the bootstrapped observations will not be stationary anymore by construction. But, it was shown that varying the block length can avoid this problem.[3]

Choice of statistic

The bootstrap distribution of a point estimator of a population parameter has been used to produce a bootstrapped confidence interval for the parameter's true value, if the parameter can be written as a function of the population's distribution.

Population parameters are estimated with many point estimators. Popular families of point-estimators include mean-unbiased minimum-variance estimators, median-unbiased estimators, Bayesian estimators (for example, the posterior distribution's mode, median, mean), and maximum-likelihood estimators.

A Bayesian point estimator and a maximum-likelihood estimator have good performance when the sample size is infinite, according to asymptotic theory. For practical problems with finite samples, other estimators may be preferable. Asymptotic theory suggests techniques that often improve the performance of bootstrapped estimators; the bootstrapping of a maximum-likelihood estimator may often be improved using transformations related to pivotal quantities.[4]

Deriving confidence intervals from the bootstrap distribution

The bootstrap distribution of a parameter-estimator has been used to calculate confidence intervals for its population-parameter.

Effect of bias and the lack of symmetry on bootstrap confidence intervals

Methods for bootstrap confidence intervals

There are several methods for constructing confidence intervals from the bootstrap distribution of a real parameter:

Example applications

Smoothed bootstrap

Simon Newcomb took observations on the speed of light.[6] The data set contains two outliers, which would greatly influence the sample mean, which need not be a consistent estimator for any population median, which need not exist for heavy-tailed distributions. The sample median is consistent and median-unbiased for the population median.

The bootstrap distribution for Newcomb's data appears below. A convolution-method of regularization reduces the discreteness of the bootstrap distribution, by adding a small amount of N(0, σ2) random noise to each bootstrap sample. A conventional choice is 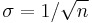\sigma = 1/\sqrt n for sample size n.

Histograms of the bootstrap distribution and the smooth bootstrap distribution appear below. The bootstrap distribution is very jagged because there are only a small number of values that the median can take. The smoothed bootstrap distribution overcomes this jaggedness.

In this example, the bootstrapped95% (percentile) confidence-interval is (26, 28.5), which is close to the interval for (25.98, 28.46) for the smoothed bootstrap.

Relation to other approaches to inference

Relationship to other resampling methods

The bootstrap is distinguished from :

For more details see bootstrap resampling.

Bootstrap aggregating (bagging) is a meta-algorithm based on averaging the results of multiple bootstrap samples.

U-statistics

Main article: U-statistic

In situations where an obvious statistic can be devised to measure a required characteristic using only a small number, r, of data items, a corresponding statistic based on the entire sample can be formulated. Given an r-sample statistic, one can create an n-sample statistic by something similar to bootstrapping (taking the average of the statistic over all subsamples of size r). This procedure is known to have certain good properties and the result is a U-statistic. The sample mean and sample variance are of this form, for r=1 and r=2.

Etymology

Although the underlying technique was introduced by Julian Simon in 1969, the use of the phrase in statistics was introduced by Bradley Efron in "Bootstrap methods: another look at the jackknife," Annals of Statistics, 7, (1979) 1-26. See Notes for Earliest Known Uses of Some of the Words of Mathematics: Bootstrap (John Aldrich) and Earliest Known Uses of Some of the Words of Mathematics (B) (Jeff Miller) for details.

See also

Notes

  1. ^ Weisstein, Eric W. "Bootstrap Methods." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BootstrapMethods.html
  2. ^ Wu, C.F.J. (1986). Jackknife, bootstrap and other resampling methods in regression analysis (with discussions). Annals of Statistics, 14, 1261-1350.
  3. ^ Politis, D.N. and Romano, J.P. (1994). The stationary bootstrap. Journal of American Statistical Association, 89, 1303-1313.
  4. ^ Davison, A. C.; Hinkley, D. V. (1997). Bootstrap methods and their application. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press. ISBN 0521573912. software. 
  5. ^ when working with small sample sizes (i.e., less than 50), the percentile confidence intervals for (for example) the variance statistic will be too narrow. So that with a sample of 20 points, 90% confidence interval will include the true variance only 78% of the time, according to Schenker.
  6. ^ Data from examples in Bayesian Data Analysis

Further reading

External links