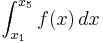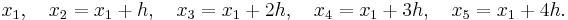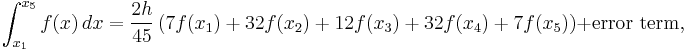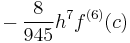Boole's rule
In mathematics, Boole's rule, named after George Boole, is a method of numerical integration. It approximates an integral
by using the values of ƒ at five equally spaced points
It is expressed thus Abramowitz and Stegun (1972, p. 886):
and the error term is
for some number c between x1 and x5. (945 = 1 × 3 × 5 × 7 × 9.)
It is often known as Bode's rule, due to a typographical error in Abramowitz and Stegun (1972, p. 886) that propagated.[1]
See also
References
- ^ Weisstein, Eric W. "Boole's Rule." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/BoolesRule.html