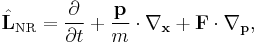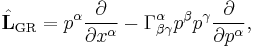Boltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas. It is one of the most important equations of non-equilibrium statistical mechanics, the area of statistical mechanics that deals with systems far from thermodynamic equilibrium; for instance, when there is an applied temperature gradient or electric field. The Boltzmann equation is used to study how a gas or fluid transports physical quantities such as heat and momentum, and thus to derive transport properties such as viscosity, and thermal conductivity. The problem of existence and uniqueness of solutions to the Boltzmann equation is still not fully resolved but the recent results are quite promising.[1][2]
Contents |
Overview
The Boltzmann equation is an equation for the time (t) evolution of the distribution (properly a density) function f(x, p, t) in one-particle phase space, where x and p are position and momentum, respectively. The distribution is defined so that
is the number of molecules which, at time t, have positions lying within a volume element 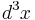 about x and momenta lying within a momentum-space element
about x and momenta lying within a momentum-space element 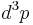 about p.[3]
about p.[3]
Consider those particles described by f experiencing an external force F. Then f must satisfy, in absence of collisions,
because particles at 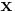 with momentum
with momentum 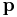 at time
at time  , will (all) be at
, will (all) be at 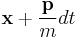 with momentum
with momentum 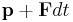 at time
at time 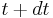 .
.
However, since collisions do occur, the particle density in the phase-space volume dx dp changes.
Dividing the equation by dx dp dt and taking the limit, we can get the Boltzmann equation
F(x, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation is often mistakenly called the Liouville equation (the Liouville Equation is an N-particle equation).
Molecular chaos and the collision term (Stosszahl Ansatz)
The above Boltzmann equation is of little practical use as it leaves the collision term unspecified. A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the 'Stosszahl Ansatz', and is also known as the 'molecular chaos assumption'. Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:
Extensions and applications
It is also possible to write down relativistic Boltzmann equations for systems in which a number of particle species can collide and produce different species. This is how the formation of the light elements in big bang nucleosynthesis is calculated. The Boltzmann equation is also often used in dynamics, especially galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe.
In Hamiltonian mechanics, the Boltzmann equation is often written more generally as
where L is the Liouville operator describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
and the generalization to (general) relativity is
where Γ is the Christoffel symbol.
See also
- H-theorem
- Fokker–Planck equation
- Navier–Stokes equations
- Vlasov equation
- Vlasov–Poisson equation
- Lattice Boltzmann methods
Notes
- ^ DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. of Math. (2) 130: 321–366.
- ^ Philip T. Gressman and Robert M. Strain (2010). "Global classical solutions of the Boltzmann equation with long-range interactions". Proceedings of the National Academy of Sciences 107 (13): 5744–5749. Bibcode 2010PNAS..107.5744G. doi:10.1073/pnas.1001185107.
- ^ Huang, Kerson (1987). Statistical Mechanics (Second ed.). New York: Wiley. p. 53. ISBN 0471815187.
References
- Arkeryd, Leif (1972). "On the Boltzmann equation part II: The full initial value problem". Arch. Rational Mech. Anal. 45: 17–34. Bibcode 1972ArRMA..45...17A. doi:10.1007/BF00253393.
- Arkeryd, Leif (1972). "On the Boltzmann equation part I: Existence". Arch. Rational Mech. Anal. 45: 1–16. Bibcode 1972ArRMA..45....1A. doi:10.1007/BF00253392.
- DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. of Math. (2) 130: 321–366.
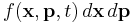
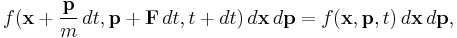
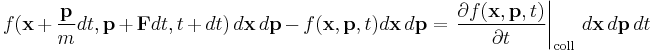
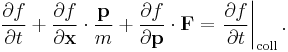
![\left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} = \int\!\!\! \int g(\mathbf{p-p'},\mathbf{q}) \left[f(\mathbf{x},\mathbf{p%2Bq},t) f(\mathbf{x},\mathbf{p'-q},t) - f(\mathbf{x},\mathbf{p},t) f(\mathbf{x},\mathbf{p'},t)\right]\,d\mathbf{p'}\,d\mathbf{q}.](/2012-wikipedia_en_all_nopic_01_2012/I/e8a8831287922e311a172221dd8d1efa.png)
![\hat{\mathbf{L}}[f]=\mathbf{C}[f], \,](/2012-wikipedia_en_all_nopic_01_2012/I/34233ea8c7799c88886b88381d2c1961.png)