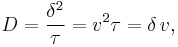Bohm diffusion
Bohm diffusion is the diffusion of plasma across a magnetic field.
Description
Bohm diffusion is charactrerized with a diffusion coefficient equal to
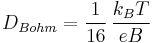 ,
,
where B is the magnetic field strength, T is the temperature, and e is the elementary charge.
It was first observed in 1949 by David Bohm, E. H. S. Burhop, and Harrie Massey while studying magnetic arcs for use in isotope separation.[1] It has since been observed that many other plasmas follow this law. Fortunately there are exceptions where the diffusion rate is lower, otherwise there would be no hope of achieving practical fusion energy. In Bohm's original work he notes that the fraction 1/16 is not exact; in particular "the exact value of [the diffusion coefficient] is uncertain within a factor of 2 or 3." Lyman Spitzer considered this fraction as a factor related to plasma instability.[2]
Generally diffusion can be modelled as a random walk of steps of length δ and time τ. If the diffusion is collisional, then δ is the mean free path and τ is the inverse of the collision frequency. The diffusion coefficient D can be expressed variously as
where v = δ/τ is the velocity between collisions.
In a magnetized plasma, the collision frequency is usually small compared to the gyrofrequency, so that the step size is the gyroradius ρ and the step time is the inverse of the collision frequency ν, leading to D = ρ²ν. If the collision frequency is larger than the gyrofrequency, then the particles can be considered to move freely with the thermal velocity vth between collisions, and the diffusion coefficient takes the form D = vth²/ν. Evidently the classical (collisional) diffusion is maximum when the collision frequency is equal to the gyrofrequency, in which case D = ρ²ωc = vth²/ωc. Substituting ρ = vth/ωc, vth = (kBT/m)1/2, and ωc = eB/m, we arrive at D = kBT/eB, which is the Bohm scaling. Considering the approximate nature of this derivation, the missing 1/16 in front is no cause for concern. Therefore, at least within a factor of order unity, Bohm diffusion is always greater than classical diffusion.
In the common low collisionality regime, classical diffusion scales with 1/B², compared with the 1/B dependence of Bohm diffusion. This distinction is often used to distinguish between the two.
In light of the calculation above, it is tempting to think of Bohm diffusion as classical diffusion with an anomalous collision rate that maximizes the transport, but the physical picture is different. Anomalous diffusion is the result of turbulence. Regions of higher or lower electric potential result in eddies because the plasma moves around them with the E-cross-B drift velocity equal to E/B. These eddies play a similar role to the gyro-orbits in classical diffusion, except that the physics of the turbulence can be such that the decorrelation time is approximately equal to the turn-over time, resulting in Bohm scaling. Another way of looking at it is that the turbulent electric field is approximately equal to the potential perturbation divided by the scale length δ, and the potential perturbation can be expected to be a sizeable fraction of the kBT/e. The turbulent diffusion constant D = δv is then independent of the scale length and is approximately equal to the Bohm value.