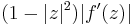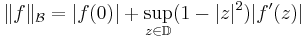Bloch space

In the mathematical field of complex analysis, the Bloch space, named after André Bloch and denoted ℬ, is the space of holomorphic functions f defined on the open unit disc D in the complex plane, such that the function

(1-|z|^2)|f^\prime(z)|

is bounded.[1] It is a Banach space, with the norm defined by

\|f\|_\mathcal{B} = |f(0)| %2B \sup_{z \in \mathbb{D}} (1-|z|^2) |f'(z)|

(Bloch norm). The elements of ℬ are called Bloch functions.

Notes

  1. ^ Wiegerinck, J. (2001), "Bloch function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=/B/b110620