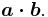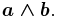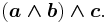Blade (geometry)
In geometric algebra, a blade is a generalization of the notion of vectors and scalars to include bivectors, trivectors, etc. In detail:[1]
- A scalar or 0-blade of grade 0 is the inner product or dot product of two vectors a and b denoted as:
- A vector is a 1-blade of grade 1.
- A 2-blade of grade 2 is a simple bivector- (sums of 2-blades also are bivectors, but may not be simple), given by the wedge product of two vectors a and b:
- A 3-blade of grade 3 is a trivector, that is, a wedge product of three vectors, a, b and c:
- A k-blade is a blade of grade k.
- The highest grade element in a space is called the pseudoscalar.[2]
- In a space of dimension n, the blade of grade n−1 is called a pseudovector.[3]
In a n-dimensional spaces, there are blades of grade zero through n. A vector space of finite dimension n is related to a pseudoscalar of grade n.[4]
Contents |
Examples
For example, in 2-dimensional space scalars are described as 0-blades, vectors are 1-blades, and area elements are 2-blades known as pseudoscalars, in that they are one-dimensional objects distinct from regular scalars.
In three-dimensional space, 0-blades are again scalars and 1-blades are three-dimensional vectors, but in three-dimensions, areas have an orientation, so while 2-blades are area elements, they are oriented. 3-blades (trivectors) represent volume elements and in three-dimensional space, these are scalar-like – i.e., 3-blades in three-dimensions form a one-dimensional vector space.
See also
Notes
- ^ Marcos A. Rodrigues (2000). "§1.2 Geometric algebra: an outline". Invariants for pattern recognition and classification. World Scientific. p. 3 ff. ISBN 9810242786. http://books.google.com/books?id=QbFSt0SlDjIC&pg=PA3.
- ^ John A. Vince (2008). Geometric algebra for computer graphics. Springer. p. 85. ISBN 1846289963. http://books.google.com/books?id=3VxZqfm3I_MC&pg=PA85&dq=pseudoscalar+%22highest+grade%22&lr=&as_drrb_is=q&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=&as_brr=0&cd=1#v=onepage&q=pseudoscalar%20%22highest%20grade%22&f=false.
- ^ William E Baylis (2004). "§4.2.3 Higher-grade multivectors in Cℓn: Duals". Lectures on Clifford (geometric) algebras and applications. Birkhäuser. p. 100. ISBN 0817632573. http://books.google.com/books?id=oaoLbMS3ErwC&pg=PA100&dq=%22pseudovectors+%28grade+n+-+1+elements%29%22&lr=&as_drrb_is=q&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=&as_brr=0&cd=1#v=onepage&q=%22pseudovectors%20%28grade%20n%20-%201%20elements%29%22&f=false.
- ^ David Hestenes (1999). New foundations for classical mechanics: Fundamental Theories of Physics. Springer. p. 54. ISBN 0792353021. http://books.google.com/books?id=AlvTCEzSI5wC&pg=PA54.
General references
- David Hestenes, Garret Sobczyk (1987). "Chapter 1: Geometric algebra". Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics. Springer. p. 1 ff. ISBN 9027725616. http://books.google.com/books?id=yyjLeKEdt20C&printsec=frontcover&source=gbs_navlinks_s#v=onepage&q=&f=false.
- Chris Doran and Anthony Lasenby (2003). Geometric algebra for physicists. Cambridge University Press. ISBN 9780521480221. http://books.google.com/books?id=nZ6MsVIdt88C&printsec=frontcover&dq=%22geometric+algebra+for+physicists%22&lr=&as_drrb_is=q&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=&as_brr=0&cd=1#v=onepage&q=&f=false.
- A Lasenby, J Lasenby & R Wareham (2004) A covariant approach to geometry using geometric algebra Technical Report. University of Cambridge Department of Engineering, Cambridge, UK.
- R Wareham, J Cameron, & J Lasenby (2005). "Applications of conformal geometric algebra to computer vision and graphics". In Hongbo Li, Peter J. Olver, Gerald Sommer. Computer algebra and geometric algebra with applications. Springer. p. 329 ff. ISBN 3540262962. http://books.google.com/books?id=uxofVAQE3LoC&pg=PA330#v=onepage&q=&f=false.
External links
- A Geometric Algebra Primer, especially for computer scientists.