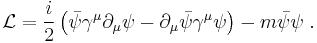Bispinor
In physics, bispinor is a four-component object which transforms under the (½,0)⊕(0,½) representation of the covariance group of special relativity[1] (see, e.g., [2]). Bispinors are used to describe relativistic spin-½ quantum fields.
In the Weyl basis a bispinor
consists of two (two-component) Weyl spinors  and
and 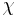 which transform, correspondingly, under (½,0) and (0,½) representations of the
which transform, correspondingly, under (½,0) and (0,½) representations of the 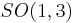 group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.
group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.
The Dirac bispinor is connected with the Weyl bispinor by a unitary transformation to the Dirac basis,
The Dirac basis is the one most widely used in the literature.
A bilinear form of bispinors 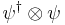 can be reduced to five irreducible (under the Lorentz group) objects:
can be reduced to five irreducible (under the Lorentz group) objects:
- scalar,
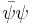 ;
; - pseudo-scalar,
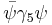 ;
; - vector,
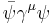 ;
; - pseudo-vector,
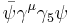 ;
; - antisymmetric tensor,
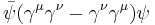 ,
,
where 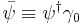 and
and 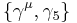 are the gamma matrices.
are the gamma matrices.
A suitable Lagrangian (the Euler-Lagrange equation of which is the Dirac equation) for the relativistic spin-½ field is given as
Notes
- ^ covariance group of special relativity is
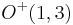 or the Lorentz group.
or the Lorentz group. - ^ Caban and Rembielinski 2005, p. 2.
References
- P. Caban and J. Rembielinski, http://arxiv.org/abs/quant-ph/0507056v1 [Phys. Rev. A 72, 012103 (2005)].
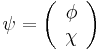
![\psi\rightarrow{1\over\sqrt2}\left[
\begin{array}{cc}1&1\\1&-1
\end{array}
\right]\psi=
{1\over\sqrt2}\left(\begin{array}{c}\phi%2B\chi\\ \phi-\chi
\end{array}\right) .](/2012-wikipedia_en_all_nopic_01_2012/I/4609c18f4769e537dcb5d0ccc22af7e7.png)