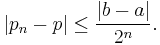Bisection method

The bisection method in mathematics is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods.[1] The method is also called the binary search method[2] and is similar to the computer science Binary Search, where the range of possible solutions is halved each iteration.

Contents

The method

The method is applicable when we wish to solve the equation f(x) = 0 for the real variable x, where f is a continuous function defined on an interval [a, b] and f(a) and f(b) have opposite signs. In this case a and b are said to bracket a root since, by the intermediate value theorem, the f must have at least one root in the interval (a, b).

At each step the method divides the interval in two by computing the midpoint c = (a+b) / 2 of the interval and the value of the function f(c) at that point. Unless c is itself a root (which is very unlikely, but possible) there are now two possibilities: either f(a) and f(c) have opposite signs and bracket a root, or f(c) and f(b) have opposite signs and bracket a root. The method selects the subinterval that is a bracket as a new interval to be used in the next step. In this way the interval that contains a zero of f is reduced in width by 50% at each step. The process is continued until the interval is sufficiently small.

Explicitly, if f(a) and f(c) are opposite signs, then the method sets c as the new value for b, and if f(b) and f(c) are opposite signs then the method sets c as the new a. (If f(c)=0 then c may be taken as the solution and the process stops.) In both cases, the new f(a) and f(b) have opposite signs, so the method is applicable to this smaller interval.[3]

Analysis

The method is guaranteed to converge to a root of f if f is a continuous function on the interval [a, b] and f(a) and f(b) have opposite signs. The absolute error is halved at each step so the method converges linearly, which is comparatively slow.

Specifically, if p1 = (a+b)/2 is the midpoint of the initial interval, and pn is the midpoint of the interval in the nth step, then the difference between pn and a solution p is bounded by[4]

|p_n-p|\le\frac{|b-a|}{2^n}.

This formula can be used to determine in advance the number of iterations that the bisection method would need to converge to a root to within a certain tolerance.

Pseudocode

The method may be written in Pseudocode as follows:[5]

INPUT: Function f, endpoint values a, b, tolerance TOL, maximum iterations NMAX
CONDITIONS: a < b, either f(a) < 0 and f(b) > 0 or f(a) > 0 and f(b) < 0
OUTPUT: value which differs from a root of f(x)=0 by less than TOL

N ← 1
While N ≤ NMAX { limit iterations to prevent infinite loop
  c ← (a + b)/2 new midpoint
  If (f(c) = 0 or (b – a)/2 < TOL then { solution found
    Output(c)
    Stop
  }
  N ← N + 1 increment step counter
  If sign(f(c)) = sign(f(a)) then a ← c else b ← c new interval
}
Output("Method failed.") max number of steps exceeded

See also

References

  1. ^ Burden & Faires p. 31
  2. ^ Burden & Faires p. 28
  3. ^ Burden & Faires p. 28 for section
  4. ^ Burden & Faires p. 31, Theorem 2.1
  5. ^ Following Burden & Faires p. 29

External links