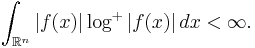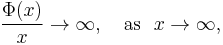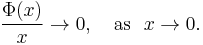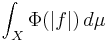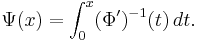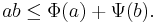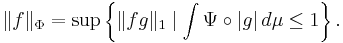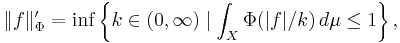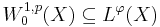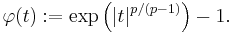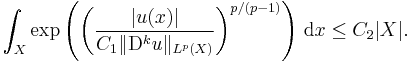Birnbaum–Orlicz space
In the mathematical analysis, and especially in real and harmonic analysis, a Birnbaum–Orlicz space is a type of function space which generalizes the Lp spaces. Like the Lp spaces, they are Banach spaces. The spaces are named for Władysław Orlicz and Zygmunt William Birnbaum, who first defined them in 1931.
Besides the Lp spaces, a variety of function spaces arising naturally in analysis are Birnbaum–Orlicz spaces. One such space L log+ L, which arises in the study of Hardy–Littlewood maximal functions, consists of measurable functions f such that the integral
Here log+ is the positive part of the logarithm. Also included in the class of Birnbaum–Orlicz spaces are many of the most important Sobolev spaces.
Contents |
Formal definition
Suppose that μ is a σ-finite measure on a set X, and Φ : [0, ∞) → [0, ∞) is a convex function such that
Let 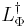 be the space of measurable functions f : X → R such that the integral
be the space of measurable functions f : X → R such that the integral
is finite, where as usual functions that agree almost everywhere are identified.
This may not be a vector space (it may fail to be closed under scalar multiplication). The vector space of functions spanned by 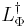 is the Birnbaum–Orlicz space, denoted
is the Birnbaum–Orlicz space, denoted 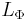 .
.
To define a norm on 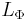 , let Ψ be the Young complement of Φ; that is,
, let Ψ be the Young complement of Φ; that is,
Note that Young's inequality holds:
The norm is then given by
Furthermore, the space 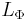 is precisely the space of measurable functions for which this norm is finite.
is precisely the space of measurable functions for which this norm is finite.
An equivalent norm (Rao & Ren 1991, §3.3) is defined on LΦ by
and likewise LΦ(μ) is the space of all measurable functions for which this norm is finite.
Properties
- Orlicz spaces generalize Lp spaces in the sense that if
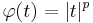 , then
, then 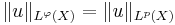 , so
, so  .
. - The Orlicz space
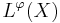 is a Banach space — a complete normed vector space.
is a Banach space — a complete normed vector space.
Relations to Sobolev spaces
Certain Sobolev spaces are embedded in Orlicz spaces: for 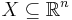 open and bounded with Lipschitz boundary
open and bounded with Lipschitz boundary 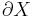 ,
,
for
This is the analytical content of the Trudinger inequality: For 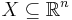 open and bounded with Lipschitz boundary
open and bounded with Lipschitz boundary 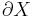 , consider the space
, consider the space 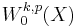 ,
, 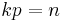 . There exist constants
. There exist constants 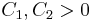 such that
such that
References
- Birnbaum, Z. W.; Orlicz, W. (1931), "Über die Verallgemeinerung des Begriffes der zueinander Konjugierten Potenzen", Studia Mathematica 3: 1–67 PDF.
- Bund, Iracema (1975), "Birnbaum–Orlicz spaces of functions on groups", Pacific Mathematics Journal 58 (2): 351–359.
- Hewitt, Edwin; Stromberg, Karl, Real and abstract analysis, Springer-Verlag.
- Krasnosel'skii, M.A.; Rutickii, Ya.B. (1961), Convex Functions and Orlicz Spaces, Groningen: P.Noordhoff Ltd
- Rao, M.M.; Ren, Z.D. (1991), Theory of Orlicz Spaces, Pure and Applied Mathematics, Marcel Dekker, ISBN 0-8247-8478-2.
- Zygmund, Antoni, "Chapter IV: Classes of functions and Fourier series", Trigonometric series, Volume 1 (3rd ed.), Cambridge University Press.