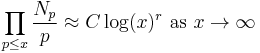Birch and Swinnerton-Dyer conjecture
| Millennium Prize Problems |
|---|
| P versus NP problem |
| Hodge conjecture |
| Poincaré conjecture |
| Riemann hypothesis |
| Yang–Mills existence and mass gap |
| Navier–Stokes existence and smoothness |
| Birch and Swinnerton-Dyer conjecture |
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay Mathematics Institute, which has offered a $1,000,000 prize for the first correct proof. As of 2011[update], only special cases of the conjecture have been proved correct.
The conjecture relates arithmetic data associated to an elliptic curve E over a number field K to the behaviour of the Hasse-Weil L-function L(E, s) of E at s = 1. More specifically, it is conjectured that the rank of the abelian group E(K) of points of E is the order of the zero of L(E, s) at s = 1, and the first non-zero coefficient in the Taylor expansion of L(E, s) at s = 1 is given by more refined arithmetic data attached to E over K.[1]
Contents |
Background
In 1922 Louis Mordell proved Mordell's theorem: the group of rational points on an elliptic curve has a finite basis. This means that for any elliptic curve there is a finite sub-set of the rational points on the curve, from which all further rational points may be generated.
If the number of rational points on a curve is infinite then some point in a finite basis must have infinite order. The number of independent basis points with infinite order is called the rank of the curve, and is an important invariant property of an elliptic curve.
If the rank of an elliptic curve is 0, then the curve has only a finite number of rational points. On the other hand, if the rank of the curve is greater than 0, then the curve has an infinite number of rational points.
Although Mordell's theorem shows that the rank of an elliptic curve is always finite, it does not give an effective method for calculating the rank of every curve. The rank of certain elliptic curves can be calculated using numerical methods but (in the current state of knowledge) these cannot be generalised to handle all curves.
An L-function L(E, s) can be defined for an elliptic curve E by constructing an Euler product from the number of points on the curve modulo each prime p. This L-function is analogous to the Riemann zeta function and the Dirichlet L-series that is defined for a binary quadratic form. It is a special case of a Hasse-Weil L-function.
The natural definition of L(E, s) only converges for values of s in the complex plane with Re(s) > 3/2. Helmut Hasse conjectured that L(E, s) could be extended by analytic continuation to the whole complex plane. This conjecture was first proved by Max Deuring for elliptic curves with complex multiplication. It was subsequently shown to be true for all elliptic curves over Q, as a consequence of the modularity theorem.
Finding rational points on a general elliptic curve is a difficult problem. Finding the points on an elliptic curve modulo a given prime p is conceptually straightforward, as there are only a finite number of possibilities to check. However, for large primes it is computationally intensive.
History
In the early 1960s Peter Swinnerton-Dyer used the EDSAC computer at the University of Cambridge Computer Laboratory to calculate the number of points modulo p (denoted by Np) for a large number of primes p on elliptic curves whose rank was known. From these numerical results Bryan Birch and Swinnerton-Dyer conjectured that Np for a curve E with rank r obeys an asymptotic law
where C is a constant.
Initially this was based on somewhat tenuous trends in graphical plots; which induced a measure of skepticism in J. W. S. Cassels (Birch's Ph.D. advisor). Over time the numerical evidence stacked up.
This in turn led them to make a general conjecture about the behaviour of a curve's L-function L(E, s) at s = 1, namely that it would have a zero of order r at this point. This was a far-sighted conjecture for the time, given that the analytic continuation of L(E, s) there was only established for curves with complex multiplication, which were also the main source of numerical examples. (NB that the reciprocal of the L-function is from some points of view a more natural object of study; on occasion this means that one should consider poles rather than zeroes.)
The conjecture was subsequently extended to include the prediction of the precise leading Taylor coefficient of the L-function at s = 1. It is conjecturally given by
where the quantities on the right hand side are invariants of the curve, studied by Cassels, Tate, Shafarevich and others: these include the order of the torsion group, the order of the Tate–Shafarevich group, and the canonical heights of a basis of rational points.[1]
Current status
The Birch and Swinnerton-Dyer conjecture has been proved only in special cases:
- In 1976, John Coates and Andrew Wiles proved that if E is a curve over a number field F with complex multiplication by an imaginary quadratic field K of class number 1, F = K or Q, and L(E, 1) is not 0 then E(F) is a finite group.[2] This was extended to the case where F is any finite abelian extension of K by Nicole Arthaud-Kuhman.[3]
- In 1983, Benedict Gross and Don Zagier showed that if a modular elliptic curve has a first-order zero at s = 1 then it has a rational point of infinite order;[4] see Gross–Zagier theorem.
- In 1990, Victor Kolyvagin showed that a modular elliptic curve E for which L(E,1) is not zero has rank 0, and a modular elliptic curve E for which L(E,1) has a first-order zero at s = 1 has rank 1.
- In 1991, Karl Rubin showed that for elliptic curves defined over an imaginary quadratic field K with complex multiplication by K, if the L-series of the elliptic curve was not zero at s=1, then the p-part of the Tate–Shafarevich group had the order predicted by the Birch and Swinnerton-Dyer conjecture, for all primes p > 7.[5]
- In 2001, Christophe Breuil, Brian Conrad, Fred Diamond and Richard Taylor, extending work of Wiles, proved that all elliptic curves defined over the rational numbers are modular (the Taniyama–Shimura theorem), which extends results 2 and 3 to all elliptic curves over the rationals, and shows that the L-functions of all elliptic curves over Q are defined at s = 1.[6]
- In 2010, Manjul Bhargava and Arul Shankar announced a proof that the average rank of the Mordell–Weil group of an elliptic curve over Q is bounded above by 7/6.[7] Combining this with the announced proof of the main conjecture of Iwasawa theory for GL(2) by Chris Skinner and Éric Urban,[8] they conclude that a positive proportion of elliptic curves over Q have analytic rank zero, and hence, by Kolyvagin's result, satisfy the Birch and Swinnerton-Dyer conjecture.
Nothing has been proved for curves with rank greater than 1, although there is extensive numerical evidence for the truth of the conjecture.
Clay Mathematics Institute Prize
The Birch and Swinnerton-Dyer conjecture is one of the seven Millennium Problems selected by the Clay Mathematics Institute, which is offering a prize of $1 million for the first proof or disproof of the whole conjecture.[9]
Notes
- ^ a b Wiles 2006
- ^ Coates, J.; Wiles, A. (1977). "On the conjecture of Birch and Swinnerton-Dyer". Inventiones Mathematicae 39 (3): 223–251. doi:10.1007/BF01402975.
- ^ Arthaud, Nicole (1978). "On Birch and Swinnerton-Dyer's conjecture for elliptic curves with complex multiplication". Compositio Mathematica 37 (2): 209–232. MR504632.
- ^ Gross, Benedict H.; Zagier, Don B. (1986). "Heegner points and derivatives of L-series". Inventiones Mathematicae 84 (2): 225–320. doi:10.1007/BF01388809. MR0833192.
- ^ Rubin, Karl (1991). "The 'main conjectures' of Iwasawa theory for imaginary quadratic fields". Inventiones Mathematicae 103 (1): 25–68. doi:10.1007/BF01239508.
- ^ Breuil, Christophe; Conrad, Brian; Diamond, Fred; Taylor, Richard (2001). "On the Modularity of Elliptic Curves over Q: Wild 3-Adic Exercises". Journal of the American Mathematical Society 14 (4): 843–939. doi:10.1090/S0894-0347-01-00370-8.
- ^ Bhargava, Manjul; Shankar, Arul (2010). Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0. arXiv:1007.0052.
- ^ Skinner, Chris; Urban, Éric (2010). "The Iwasawa main conjectures for GL2". In preparation. http://www.math.columbia.edu/~urban/eurp/MC.pdf.
- ^ Birch and Swinnerton-Dyer Conjecture at Clay Mathematics Institute
References
- Wiles, Andrew (2006), "The Birch and Swinnerton-Dyer conjecture", in Carlson, James; Jaffe, Arthur; Wiles, Andrew, The Millennium prize problems, American Mathematical Society, pp. 31–44, ISBN 978-0-821-83679-8, http://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/birchswin.pdf
External links
- Weisstein, Eric W., "Swinnerton-Dyer Conjecture" from MathWorld.
- Birch and Swinnerton-Dyer Conjecture on PlanetMath
- The Birch and Swinnerton-Dyer Conjecture: An Interview with Professor Henri Darmon by Agnes F. Beaudry
|
||||||||||||||||||||