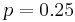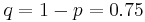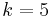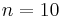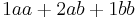Binomial probability
Binomial probability typically deals with the probability of several successive decisions, each of which has two possible outcomes.
Contents |
Definition
The probability of an event can be expressed as a binomial probability if its outcomes can be broken down into two probabilities p and q, where p and q are complementary (i.e. p + q = 1) For example, tossing a coin can be either heads or tails, each which have a (theoretical) probability of 0.5. Rolling a four on a six-sided die can be expressed as the probability (1/6) of getting a 4, or the probability (5/6) of rolling something else.
Calculation
If an event has a probability, p, of happening, then the probability of it happening twice is p2, and in general pn for n successive trials. If we want to know the probability of rolling a die three times and getting two fours and one other number (in that specific order) it becomes: P(2 rolls of 4 and 1 roll of another) = P(2 rolls of 4)×P(1 roll of another). Simplifying this give P(rolling a 4)2×P(rolling another). Using basic proability this become (1/6)2×(5/6) = 5/216.
However, this is only sufficient for problems where the order is specific. If order is not important in the above example, then there are 3 ways that 2 rolls of four and 1 other could occur: (4–4–another), (4–another–4) and (another–4–4). Since there are 3 ways of achieving the same goal, the probability is 3 times that of before, i.e. 15/216 = 5/72. If order does not matter, then there are 3C2 possible configurations, where 3C2 = 3. In what follows, we use 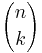 to denote nCr.
to denote nCr.
General equation
The probability of getting exactly  successes in
successes in  trials is
trials is
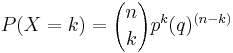
where  is the probability of a success,
is the probability of a success,  is
is 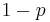 , or the probability of a failure, and
, or the probability of a failure, and
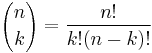 .
.
The value of  is complementary to
is complementary to  , that is
, that is 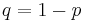 . The expression appears also in the binomial theorem.
. The expression appears also in the binomial theorem.
Example
On a 10 question multiple choice test, with 4 options per question, the probability of getting exactly 5 answers correct if the answers are guessed can be calculated like so:
Therefore if somebody guesses 10 answers on a multiple choice test with 4 options, they have about a 5.8% chance of getting 5 and only 5 correct answers. If 5 or more correct answers are needed to pass, then the probability of passing can be calculated by adding the probability of getting 5 (and only 5) answers correct, 6 (and only 6) answers correct, and so on up to 10 answers correct. The total probability of 5 or more correct answers is approximately 7.8%.
Estimation
There are various methods at estimating the binomial probability if the exponents are too large to calculate
Binomial approximation
One method is by approximating the probability to a normal distribution. The requirements are that 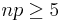 and
and 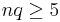 for an accurate answer. Approximation is done with the following equation:
for an accurate answer. Approximation is done with the following equation:
Where 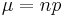 and
and 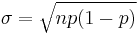 (the standard deviation of the binomial approximation) and z is the corresponding z-score.
(the standard deviation of the binomial approximation) and z is the corresponding z-score.
Poisson probability function
Another possible method is approximating to a Poisson distribution. The requirements are that 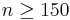 and that np and npq are within 10% of each other. The formula is
and that np and npq are within 10% of each other. The formula is
where 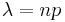 .
.
Connection to binomial theorem
The equation for binomial probability is the same as the binomial theorem equation, which can be used to calculate terms in Pascal's triangle and the expansion of binomial equations of the form 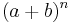 . So, if the binomial is expanded for n = 2, we get
. So, if the binomial is expanded for n = 2, we get
Rewriting the equation in a trivial way:
If a represents heads and b tails, then the above shows all the possibilities and the number of possible combinations. That is, there is one way to get two heads (aa), two ways to get a head and a tail (2ab) and one way to get two tails (bb) This applies for any degree of n. Since the sum of the coefficients in the equation (a0 + a1 + a2) is the total possibilities, and since each unique case has the same probability, the probability of getting 1 occurrence of a and 1 of b (1 head and 1 tail on a coin) is 2 out of 4, or 0.5. The sum of coefficients for any binomial is 2n.
See also
- Probability
- Binomial theorem
- Pascal's triangle
- Complementary event
- Binomial distribution
- Poisson distribution