Binary search tree

Binary Search Tree
Type Tree
Time complexity
in big O notation
Average Worst case
Space O(n) O(n)
Search O(log n) O(n)
Insert O(log n) O(n)
Delete O(log n) O(n)

In computer science, a binary search tree (BST), which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structure which has the following properties:[1]

Generally, the information represented by each node is a record rather than a single data element. However, for sequencing purposes, nodes are compared according to their keys rather than any part of their associated records.

The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient.

Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.

Contents

Operations

Operations on a binary search tree require comparisons between nodes. These comparisons are made with calls to a comparator, which is a subroutine that computes the total order (linear order) on any two values. This comparator can be explicitly or implicitly defined, depending on the language in which the BST is implemented.

Searching

Searching a binary search tree for a specific value can be a recursive or iterative process. This explanation covers a recursive method.

We begin by examining the root node. If the tree is null, the value we are searching for does not exist in the tree. Otherwise, if the value equals the root, the search is successful. If the value is less than the root, search the left subtree. Similarly, if it is greater than the root, search the right subtree. This process is repeated until the value is found or the indicated subtree is null. If the searched value is not found before a null subtree is reached, then the item must not be present in the tree.

Here is the search algorithm in the Python programming language:

# 'node' refers to the parent-node in this case
 def search_binary_tree(node, key):
     if node is None:
         return None  # key not found
     if key < node.key:
         return search_binary_tree(node.leftChild, key)
     elif key > node.key:
         return search_binary_tree(node.rightChild, key)
     else:  # key is equal to node key
         return node.value  # found key

… or equivalent Haskell:

 searchBinaryTree _   NullNode = Nothing
 searchBinaryTree key (Node nodeKey nodeValue (leftChild, rightChild)) =
     case compare key nodeKey of
       LT -> searchBinaryTree key leftChild
       GT -> searchBinaryTree key rightChild
       EQ -> Just nodeValue

This operation requires O(log n) time in the average case, but needs O(n) time in the worst case, when the unbalanced tree resembles a linked list (degenerate tree).

Assuming that BinarySearchTree is a class with a member function "search(int)" and a pointer to the root node, the algorithm is also easily implemented in terms of an iterative approach. The algorithm enters a loop, and decides whether to branch left or right depending on the value of the node at each parent node.

bool BinarySearchTree::search(int val)
{
    Node *next = this->root();
 
    while (next != NULL) {
        if (val == next->value()) {
            return true;
        } else if (val < next->value()) {
            next = next->left();   
        } else {
            next = next->right();
        }
    } 
 
    //not found
    return false;
}

Insertion

Insertion begins as a search would begin; if the root is not equal to the value, we search the left or right subtrees as before. Eventually, we will reach an external node and add the value as its right or left child, depending on the node's value. In other words, we examine the root and recursively insert the new node to the left subtree if the new value is less than the root, or the right subtree if the new value is greater than or equal to the root.

Here's how a typical binary search tree insertion might be performed in C++:

 /* Inserts the node pointed to by "newNode" into the subtree rooted at "treeNode" */
 void InsertNode(Node* &treeNode, Node *newNode)
 {
     if (treeNode == NULL)
       treeNode = newNode;
     else if (newNode->key < treeNode->key)
       InsertNode(treeNode->left, newNode);
     else
       InsertNode(treeNode->right, newNode);
 }

The above "destructive" procedural variant modifies the tree in place. It uses only constant space, but the previous version of the tree is lost. Alternatively, as in the following Python example, we can reconstruct all ancestors of the inserted node; any reference to the original tree root remains valid, making the tree a persistent data structure:

 def binary_tree_insert(node, key, value):
     if node is None:
         return TreeNode(None, key, value, None)
     if key == node.key:
         return TreeNode(node.left, key, value, node.right)
     if key < node.key:
         return TreeNode(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
     else:
         return TreeNode(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))

The part that is rebuilt uses Θ(log n) space in the average case and O(n) in the worst case (see big-O notation).

In either version, this operation requires time proportional to the height of the tree in the worst case, which is O(log n) time in the average case over all trees, but O(n) time in the worst case.

Another way to explain insertion is that in order to insert a new node in the tree, its value is first compared with the value of the root. If its value is less than the root's, it is then compared with the value of the root's left child. If its value is greater, it is compared with the root's right child. This process continues, until the new node is compared with a leaf node, and then it is added as this node's right or left child, depending on its value.

There are other ways of inserting nodes into a binary tree, but this is the only way of inserting nodes at the leaves and at the same time preserving the BST structure.

Here is an iterative approach to inserting into a binary search tree in Java:

private Node m_root;
 
public void insert(int data) {
    if (m_root == null) {
        m_root = new TreeNode(data, null, null);
        return;
    }
    Node root = m_root;
    while (root != null) {
        // Not the same value twice
        if (data == root.getData()) {
            return;
        } else if (data < root.getData()) {
            // insert left
            if (root.getLeft() == null) {
                root.setLeft(new TreeNode(data, null, null));
                return;
            } else {
                root = root.getLeft();
            }
        } else {
            // insert right
            if (root.getRight() == null) {
                root.setRight(new TreeNode(data, null, null));
                return;
            } else {
                root = root.getRight();
            }
        }
    }
}

Below is a recursive approach to the insertion method.

private Node m_root;
 
public void insert(int data){
    if (m_root == null) {
        m_root = TreeNode(data, null, null);	
    }else{
        internalInsert(m_root, data);
    }
}
 
private static void internalInsert(Node node, int data){
    // Not the same value twice
    if (data == node.getValue()) {
        return;
    } else if (data < node.getValue()) {
        if (node.getLeft() == null) {
            node.setLeft(new TreeNode(data, null, null));
        }else{
            internalInsert(node.getLeft(), data);
        }
    }else{
        if (node.getRight() == null) {
            node.setRight(new TreeNode(data, null, null));
        }else{
            internalInsert(node.getRight(), data);
        }	
    }
}

Deletion

There are three possible cases to consider:

As with all binary trees, a node's in-order successor is the left-most child of its right subtree, and a node's in-order predecessor is the right-most child of its left subtree. In either case, this node will have zero or one children. Delete it according to one of the two simpler cases above.

Consistently using the in-order successor or the in-order predecessor for every instance of the two-child case can lead to an unbalanced tree, so good implementations add inconsistency to this selection.

Running Time Analysis: Although this operation does not always traverse the tree down to a leaf, this is always a possibility; thus in the worst case it requires time proportional to the height of the tree. It does not require more even when the node has two children, since it still follows a single path and does not visit any node twice.

Here is the code in Python:

def findMin(self):
    '''
    Finds the smallest element that is a child of *self*
    '''
    current_node = self
    while current_node.left_child:
        current_node = current_node.left_child
    return current_node
 
def replace_node_in_parent(self, new_value=None):
    '''
    Removes the reference to *self* from *self.parent* and replaces it with *new_value*.
    '''
    if self.parent:
        if self == self.parent.left_child:
            self.parent.left_child = new_value
        else:
            self.parent.right_child = new_value
    if new_value:
        new_value.parent = self.parent
 
def binary_tree_delete(self, key):
    if key < self.key:
        self.left_child.binary_tree_delete(key)
    elif key > self.key:
        self.right_child.binary_tree_delete(key)
    else: # delete the key here
        if self.left_child and self.right_child: # if both children are present
            # get the smallest node that's bigger than *self*
            successor = self.right_child.findMin()
            self.key = successor.key
            # if *successor* has a child, replace it with that
            # at this point, it can only have a *right_child*
            # if it has no children, *right_child* will be "None"
            successor.replace_node_in_parent(successor.right_child)
        elif self.left_child or self.right_child:   # if the node has only one child
            if self.left_child:
                self.replace_node_in_parent(self.left_child)
            else:
                self.replace_node_in_parent(self.right_child)
        else: # this node has no children
            self.replace_node_in_parent(None)

Source code in C++ (from http://www.algolist.net/Data_structures/Binary_search_tree). This URL also explains the operation nicely using diagrams.

bool BinarySearchTree::remove(int value) {
  if (root == NULL)
    return false;
  else {
    if (root->getValue() == value) {
      BSTNode auxRoot(0);
      auxRoot.setLeftChild(root);
      BSTNode* removedNode = root->remove(value, &auxRoot);
      root = auxRoot.getLeft();
      if (removedNode != NULL) {
        delete removedNode;
        return true;
      } else
        return false;
    } else {
      BSTNode* removedNode = root->remove(value, NULL);
      if (removedNode != NULL) {
        delete removedNode;
        return true;
      } else
        return false;
    }
  }
}
 
BSTNode* BSTNode::remove(int value, BSTNode *parent) {
  if (value < this->value) {
    if (left != NULL)
      return left->remove(value, this);
    else
      return NULL;
  } else if (value > this->value) {
    if (right != NULL)
      return right->remove(value, this);
    else
      return NULL;
  } else {
    if (left != NULL && right != NULL) {
      this->value = right->minValue();
      return right->remove(this->value, this);
    } else if (parent->left == this) {
      parent->left = (left != NULL) ? left : right;
      return this;
    } else if (parent->right == this) {
      parent->right = (left != NULL) ? left : right;
      return this;
    }
  }
}
 
int BSTNode::minValue() {
  if (left == NULL)
    return value;
  else
    return left->minValue();
}

Traversal

Main article: Tree traversal

Once the binary search tree has been created, its elements can be retrieved in-order by recursively traversing the left subtree of the root node, accessing the node itself, then recursively traversing the right subtree of the node, continuing this pattern with each node in the tree as it's recursively accessed. As with all binary trees, one may conduct a pre-order traversal or a post-order traversal, but neither are likely to be useful for binary search trees.

The code for in-order traversal in Python is given below. It will call callback for every node in the tree.

def traverse_binary_tree(node, callback):
    if node is None:
        return
    traverse_binary_tree(node.leftChild, callback)
    callback(node.value)
    traverse_binary_tree(node.rightChild, callback)

Traversal requires Ω(n) time, since it must visit every node. This algorithm is also O(n), so it is asymptotically optimal.

The Code for in-order traversal in Language C is given below.

void InOrderTraversal(struct Node *n)
{
	struct Node *Cur, *Pre;
	if(n==NULL)
		return;
 
	Cur = n;
	while(Cur != NULL)
	{
		if(Cur->lptr == NULL)
		{
			printf("\t%d",Cur->val);
			Cur= Cur->rptr;
		}
		else
		{
			Pre = Cur->lptr;
			while(Pre->rptr !=NULL && Pre->rptr != Cur)
				Pre = Pre->rptr;
 
			if (Pre->rptr == NULL)
			{
				Pre->rptr = Cur;
				Cur = Cur->lptr;
			}
			else
			{
				Pre->rptr = NULL;
				printf("\t%d",Cur->val);
				Cur = Cur->rptr;
			}
		}
	}
}

Sort

A binary search tree can be used to implement a simple but efficient sorting algorithm. Similar to heapsort, we insert all the values we wish to sort into a new ordered data structure—in this case a binary search tree—and then traverse it in order, building our result:

def build_binary_tree(values):
    tree = None
    for v in values:
        tree = binary_tree_insert(tree, v)
    return tree
 
def get_inorder_traversal(root):
    '''
    Returns a list containing all the values in the tree, starting at *root*.
    Traverses the tree in-order(leftChild, root, rightChild).
    '''
    result = []
    traverse_binary_tree(root, lambda element: result.append(element))
    return result

The worst-case time of build_binary_tree is 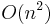O(n^2)—if you feed it a sorted list of values, it chains them into a linked list with no left subtrees. For example, build_binary_tree([1, 2, 3, 4, 5]) yields the tree (1 (2 (3 (4 (5))))).

There are several schemes for overcoming this flaw with simple binary trees; the most common is the self-balancing binary search tree. If this same procedure is done using such a tree, the overall worst-case time is O(nlog n), which is asymptotically optimal for a comparison sort. In practice, the poor cache performance and added overhead in time and space for a tree-based sort (particularly for node allocation) make it inferior to other asymptotically optimal sorts such as heapsort for static list sorting. On the other hand, it is one of the most efficient methods of incremental sorting, adding items to a list over time while keeping the list sorted at all times.

Types

There are many types of binary search trees. AVL trees and red-black trees are both forms of self-balancing binary search trees. A splay tree is a binary search tree that automatically moves frequently accessed elements nearer to the root. In a treap ("tree heap"), each node also holds a (randomly chosen) priority and the parent node has higher priority than its children. Tango Trees are trees optimized for fast searches.

Two other titles describing binary search trees are that of a complete and degenerate tree.

A complete tree is a tree with n levels, where for each level d <= n - 1, the number of existing nodes at level d is equal to 2d. This means all possible nodes exist at these levels. An additional requirement for a complete binary tree is that for the nth level, while every node does not have to exist, the nodes that do exist must fill from left to right.

A degenerate tree is a tree where for each parent node, there is only one associated child node. What this means is that in a performance measurement, the tree will essentially behave like a linked list data structure.

Performance comparisons

D. A. Heger (2004)[2] presented a performance comparison of binary search trees. Treap was found to have the best average performance, while red-black tree was found to have the smallest amount of performance fluctuations.

Optimal binary search trees

If we don't plan on modifying a search tree, and we know exactly how often each item will be accessed, we can construct an optimal binary search tree, which is a search tree where the average cost of looking up an item (the expected search cost) is minimized.

Even if we only have estimates of the search costs, such a system can considerably speed up lookups on average. For example, if you have a BST of English words used in a spell checker, you might balance the tree based on word frequency in text corpora, placing words like "the" near the root and words like "agerasia" near the leaves. Such a tree might be compared with Huffman trees, which similarly seek to place frequently-used items near the root in order to produce a dense information encoding; however, Huffman trees only store data elements in leaves and these elements need not be ordered.

If we do not know the sequence in which the elements in the tree will be accessed in advance, we can use splay trees which are asymptotically as good as any static search tree we can construct for any particular sequence of lookup operations.

Alphabetic trees are Huffman trees with the additional constraint on order, or, equivalently, search trees with the modification that all elements are stored in the leaves. Faster algorithms exist for optimal alphabetic binary trees (OABTs).

Example:

procedure Optimum Search Tree(f, f´, c):
 for j = 0 to n do
  c[j, j] = 0, F[j, j] = f´j
  for d = 1 to n do
   for i = 0 to (n − d) do
    j = i + d
    F[i, j] = F[i, j − 1] + f´ + f´j
    c[i, j] = MIN(i<k<=j){c[i, k − 1] + c[k, j]} + F[i, j]

See also

References

  1. ^ Gilberg, R.; Forouzan, B. (2001), "8", Data Structures: A Pseudocode Approach With C++, Pacific Grove, CA: Brooks/Cole, p. 339, ISBN 0-534-95216-X 
  2. ^ Heger, Dominique A. (2004), "A Disquisition on The Performance Behavior of Binary Search Tree Data Structures", European Journal for the Informatics Professional 5 (5): 67–75, http://www.cepis.org/upgrade/files/full-2004-V.pdf 

Further reading

External links

Binary trees
Binary search tree (BST) · Cartesian tree · Top tree · T-tree
Self-balancing binary search trees
B-trees
Tries
Binary space partitioning (BSP) trees
Non-binary trees
Spatial data partitioning trees
Other trees
Types
Abstract
Arrays
Linked
Trees
Graphs