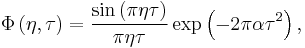Bilinear time–frequency distribution
Bilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data. Such methods are used where one needs to deal with a situation where the frequency composition of a signal may be changing over time; this sub-field used to be called time–frequency signal analysis, and is now more often called time–frequency signal processing due to the progress in using these methods to a wide range of signal-processing problems.
Contents |
Background
Methods for analysing time series, in both signal analysis and time series analysis, have been developed as essentially separate methodologies applicable to, and based in, either the time or the frequency domain. A mixed approach is required in time–frequency analysis techniques which are especially effective in analyzing non-stationary signals, whose frequency distribution and magnitude vary with time. Examples of these are acoustic signals. Classes of "quadratic time-frequency distributions" (or bilinear time–frequency distributions") are used for time–frequency signal analysis. This class is similar in formulation to Cohen's class distribution function that was used in 1966 in the context of quantum mechanics. This distribution function is mathematically similar to a generalized time–frequency representation which utilizes bilinear transformations. Compared with other time–frequency analysis techniques, such as short-time Fourier transform (STFT), the bilinear-transformation (or quadratic time–frequency distributions) may not have higher clarity for most practical signals, but it provides an alternative framework to investigate new definitions and new methods. While it does suffer from an inherent cross-term contamination when analyzing multi-component signals, by using a carefully chosen window functions, the interference can be significantly mitigated, at the expense of resolution.
Mathematical definition
The definition of the class of bilinear (or quadratic) time–frequency distributions is as follows:
where  is the ambiguity function (AF) which will be further discussed later, and
is the ambiguity function (AF) which will be further discussed later, and  is the kernel function which is usually a low-pass function and is used to mask out the interference.
is the kernel function which is usually a low-pass function and is used to mask out the interference.
Ambiguity function
The class of bilinear (or quadratic) time–frequency distributions can be most easily understood in terms of the ambiguity function an explanation of which follows.
Consider the well known power spectral density  and the signal auto-correlation function
and the signal auto-correlation function 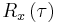 in the case of a stationary process. The relationship between these functions is as follows:
in the case of a stationary process. The relationship between these functions is as follows:
For a non-stationary signal 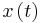 , these relations can be generalized using a time-dependent power spectral density or equivalently the famous Wigner distribution function of
, these relations can be generalized using a time-dependent power spectral density or equivalently the famous Wigner distribution function of 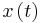 as follows:
as follows:
If the Fourier transform of the auto-correlation function is taken with respect to  instead of
instead of  , we get the ambiguity function as follows:
, we get the ambiguity function as follows:
The relationship between the Wigner distribution function, the auto-correlation function and the ambiguity function can then be illustrated by the following figure.
By comparing the definition of bilinear (or quadratic) time–frequency distributions with that of the Wigner distribution function, it is easily found that the latter is a special case of the former with 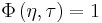 . Alternatively, bilinear (or quadratic) time–frequency distributions can be regarded as a masked version of the Wigner distribution function if a kernel function
. Alternatively, bilinear (or quadratic) time–frequency distributions can be regarded as a masked version of the Wigner distribution function if a kernel function 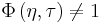 is chosen. A properly chosen kernel function can significantly reduce the undesirable cross-term of the Wigner distribution function.
is chosen. A properly chosen kernel function can significantly reduce the undesirable cross-term of the Wigner distribution function.
What is the benefit of the additional kernel function? The following figure shows the distribution of the auto-term and the cross-term of a multi-component signal in both the ambiguity and the Wigner distribution function.
For multi-component signals in general, the distribution of its auto-term and cross-term within its Wigner distribution function is generally not predictable, and hence the cross-term cannot be removed easily. However, as shown in the figure, for the ambiguity function, the auto-term of the multi-component signal will inherently tend to close the origin in the 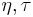 plane, and the cross-term will tend to be away from the origin. With this property, the cross-term in can be filtered out effortlessly if a proper low-pass kernel function is applied in
plane, and the cross-term will tend to be away from the origin. With this property, the cross-term in can be filtered out effortlessly if a proper low-pass kernel function is applied in 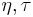 domain. The following is an example that demonstrates how the cross-term is filtered out.
domain. The following is an example that demonstrates how the cross-term is filtered out.
Some time-frequency distributions
Wigner distribution function
Aforementioned, the Wigner distribution function is a member of the class of quadratic time-frequency distributions (QTFDs)with the kernel function 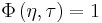 . The definition of Wigner distribution is as follows:
. The definition of Wigner distribution is as follows:
Choi–Williams distribution function
The kernel of Choi–Williams distribution is defined as follows:
where α is an adjustable parameter.
Cone-shape distribution function
The kernel of cone-shape distribution function is defined as follows:
where  is an adjustable parameter. See Transformation between distributions in time-frequency analysis. More such QTFDs and a full list can be found in, e.g., Cohen's text cited.
is an adjustable parameter. See Transformation between distributions in time-frequency analysis. More such QTFDs and a full list can be found in, e.g., Cohen's text cited.
References
- B. Boashash, "Note on the Use of the Wigner Distribution for Time Frequency Signal Analysis", IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 9, pp. 1518–1521, Sept. 1988
- B. Boashash, editor, “Time-Frequency Signal Analysis and Processing – A Comprehensive Reference”, Elsevier Science, Oxford, 2003.
- Jian-Jiun Ding, Time frequency analysis and wavelet transform class note,the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.
- S. Qian and D. Chen, Joint Time-Frequency Analysis: Methods and Applications, Chap. 5, Prentice Hall, N.J., 1996.
- L. Cohen, Time-Frequency Analysis, Prentice-Hall, New York, 1995.
- H. Choi and W. J. Williams, “Improved time-frequency representation of multicomponent signals using exponential kernels,” IEEE. Trans. Acoustics, Speech, Signal Processing, vol. 37, no. 6, pp. 862–871, June 1989.
- Y. Zhao, L. E. Atlas, and R. J. Marks, “The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals,” IEEE Trans. Acoustics, Speech, Signal Processing, vol. 38, no. 7, pp. 1084–1091, July 1990.
- L. Cohen, “Time-Frequency Distributions—A Review,” Proceedings of the IEEE, vol. 77, no. 7, pp. 941–981, 1989.
- B. Boashash, “Time-Frequency Concepts”, Chapter 1, pp. 3–28, in B. Boashash, ed,, Time-Frequency Signal Analysis & Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.
- B. Boashash, “Heuristic Formulation of Time-Frequency Distributions”, Chapter 2, pp. 29–58, in B. Boashash, editor, Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.
- B. Boashash, “Theory of Quadratic TFDs”, Chapter 3, pp. 59–82, in B. Boashash, editor, Time-Frequency Signal Analysis & Processing: A Comprehensive Reference, Elsevier, Oxford, 2003.
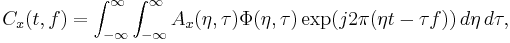
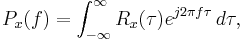
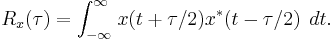
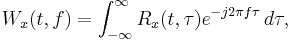
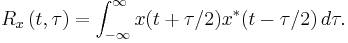
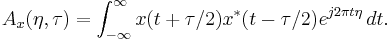
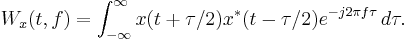
![\Phi \left(\eta,\tau \right) = \exp \left[-\alpha \left(\eta \tau \right)^2 \right], \,](/2012-wikipedia_en_all_nopic_01_2012/I/3512863a5df2c8635eaeb7f512ff45a1.png)