Biholomorphism

In the mathematical theory of functions of one or more complex variables, and also in complex algebraic geometry, a biholomorphism or biholomorphic function is a bijective holomorphic function whose inverse is also holomorphic.

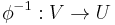Formally, a biholomorphic function is a function $\phi$ defined on an open subset U of the $n$ -dimensional complex space Cⁿ with values in Cⁿ which is holomorphic and one-to-one, such that its image is an open set $V$ in Cⁿ and the inverse $\phi^{-1}:V\to U$ is also holomorphic. More generally, U and V can be complex manifolds. One can prove that it is enough for $\phi$ to be holomorphic and one-to-one in order for it to be biholomorphic onto its image.

If there exists a biholomorphism 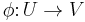$\phi \colon U \to V$ , we say that U and V are biholomorphically equivalent or that they are biholomorphic.

If 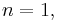$n=1,$ every simply connected open set other than the whole complex plane is biholomorphic to the unit disc (this is the Riemann mapping theorem). The situation is very different in higher dimensions. For example, open unit balls and open unit polydiscs are not biholomorphically equivalent for 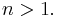$n>1.$ In fact, there does not exist even a proper holomorphic function from one to the other.

In the case of the complex plane C, some authors (e.g. Freitag 2009, Definition IV.4.1) define conformal map as a synonym for biholomorphism. The usual conditions for a function $\phi$ to be conformal on C - namely, that $\phi$ is holomorphic and that its derivative is nowhere zero - are equivalent to biholomorphism.

References

Steven G. Krantz (2002). Function Theory of Several Complex Variables. American Mathematical Society. ISBN 0-8218-2724-3.
John P. D'Angelo (1993). Several Complex Variables and the Geometry of Real Hypersurfaces. CRC Press. ISBN 0-8493-8272-6.
Eberhard Freitag and Rolf Busam (2009). Complex Analysis. Springer-Verlag. ISBN 978-3-540-93982-5.

This article incorporates material from biholomorphically equivalent on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.