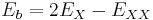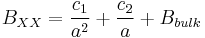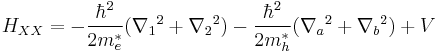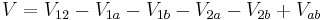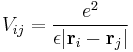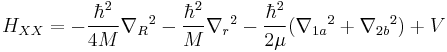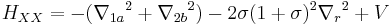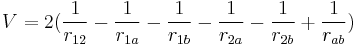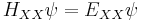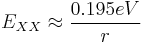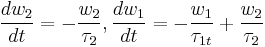Biexciton
Biexcitons are created from two free excitons.
Contents |
Formation of biexcitons
In quantum information and computation, it is essential to construct coherent combinations of quantum states. The basic quantum operations can be performed on a sequence of pairs of physically distinguishable quantum bits and, therefore, can be illustrated by a simple four-level system.
In an optically driven system where the 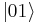 and
and  states can be directly excited, direct excitation of the upper
states can be directly excited, direct excitation of the upper 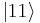 level from the ground state
level from the ground state 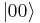 is usually forbidden and the most efficient alternative is coherent nondegenerate two-photon excitation, using
is usually forbidden and the most efficient alternative is coherent nondegenerate two-photon excitation, using 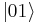 or
or  as an intermediate state. [1] [2]
as an intermediate state. [1] [2]
At high exciton densities in some materials, the formation of exciton molecules called biexcitons is also observed. This is the equivalent process to the formation of an 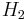 molecule from two isolated hydrogen atoms.
molecule from two isolated hydrogen atoms.
Biexcitons have been observed in a number of compound semiconductors, including CdS, ZnSe, ZnO and especially copper chloride. CuCl has a band gap at 3.40 eV, and the ground state exciton is observed at 3.20 eV, implying that Rx = 0.2 eV. At high densities, a new feature is observed in the absorption spectrum at 3.18 eV. This is attributed to biexciton formation. The energy difference between the two features tells us that the binding energy of the biexciton is 0.02 eV.
Attempts to observe biexcitons in materials like GaAs have been hindered by the nonlinear saturation effects described. [3]
Observation of biexcitons
Three possibilities of observing biexcitons exist: [4]
(a) excitation from the one-exciton band to the biexciton band (pump-probe experiments);
(b) two-photon absorption of light from the ground state to the biexciton state;
(c) luminescence from a biexciton state made up from two free excitons in a dense exciton system.
Binding energy of biexcitons
The biexciton is a quasi-particle formed from two excitons, and its energy is expressed as
where 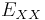 is the biexciton energy,
is the biexciton energy, 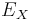 is the exciton energy, and
is the exciton energy, and
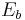 is the biexciton binding energy.
is the biexciton binding energy.
When a biexciton is annihilated, it disintegrates into a free exciton and a photon. The energy of the photon is smaller than that of the biexciton by the biexciton binding energy, so the biexciton luminescence peak appears on the low-energy side of the exciton peak. See Figure 1 in Reference 8.
The biexciton binding energy in semiconductor quantum dots has been the subject of extensive theoretical study. Because a biexciton is a composite of two electrons and two holes, we must solve a four-body problem under spatially restricted conditions. The biexciton binding energies for CuCl quantum dots, as measured by the site selective luminescence method, increased with decreasing quantum dot size. The data were well fitted by the function
where 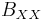 is biexciton binding energy,
is biexciton binding energy,  is the radius of the quantum dots,
is the radius of the quantum dots, 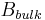 is the binding energy of bulk crystal, and
is the binding energy of bulk crystal, and 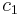 and
and 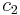 are fitting parameters. [5]
are fitting parameters. [5]
A simple model for describing binding energy of biexcitons
In the effective-mass approximation, the Hamiltonian of the system consisting of two electrons (1, 2) and two holes (a, b) is given by
where 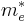 and
and 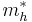 are the effective masses of electrons and holes, respectively, and
are the effective masses of electrons and holes, respectively, and
where 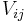 denotes the Coulomb interaction between the charged particles
denotes the Coulomb interaction between the charged particles  and
and  (
(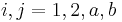 denote the two electrons and two holes in the biexciton) given by
denote the two electrons and two holes in the biexciton) given by
where  is the dielectric constant of the material.
is the dielectric constant of the material.
Denoting 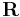 and
and 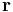 are the c.m. coordinate and the relative coordinate of the biexciton, respectively, and
are the c.m. coordinate and the relative coordinate of the biexciton, respectively, and 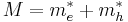 is the effective mass of the exciton, the Hamiltonian becomes
is the effective mass of the exciton, the Hamiltonian becomes
where 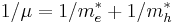 ;
; 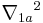 and
and 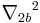 are the Laplacians with respect to relative coordinates between electron and hole, respectively. And
are the Laplacians with respect to relative coordinates between electron and hole, respectively. And 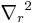 is that with respect to relative coordinate between the c. m. of excitons, and
is that with respect to relative coordinate between the c. m. of excitons, and 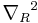 is that with respect to the c. m. coordinate
is that with respect to the c. m. coordinate 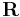 of the system.
of the system.
In the units of the exciton Rydberg and Bohr radius, the Hamiltonian can be written in dimensionless form
where 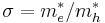 with neglecting kinetic energy operator of c. m. motion. And
with neglecting kinetic energy operator of c. m. motion. And  can be written as
can be written as
To solve the problem of the bound states of the biexciton complex, it is required to find the wave functions  satisfying the wave equation
satisfying the wave equation
If the eigenvalue 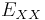 can be obtained, the binding energy of the biexciton can be also acquired
can be obtained, the binding energy of the biexciton can be also acquired
where 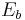 is the binding energy of the biexciton and
is the binding energy of the biexciton and 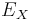 is the energy of exciton. [6]
is the energy of exciton. [6]
Binding energy in nanotubes
Biexcitons with bound complexes formed by two excitons are surprisingly stable for carbon nanotube in a wide diameter range. Thus, a biexciton binding energy exceeding the inhomogeneous exciton line width is predicted for a wide range of nanotubes.
The biexciton binding energy in carbon nanotube is quite accurately approximated by an inverse dependence on  , except perhaps for the smallest values of
, except perhaps for the smallest values of  .
.
The actual biexciton binding energy is inversely proportional to the physical nanotube radius. [7]
Binding energy in CuCl QDs
The binding energy of biexcitons increase with the decrease in their size and its size dependence and bulk value are well represented by the expression
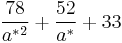 (meV)
(meV)
where 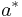 is the effective radius of microcrystallites in a unit of nm. The enhanced Coulomb interaction in microcrystallites still increase the biexciton binding energy in the large-size regime, where the quantum confinement energy of excitons is not considerable. [8]
is the effective radius of microcrystallites in a unit of nm. The enhanced Coulomb interaction in microcrystallites still increase the biexciton binding energy in the large-size regime, where the quantum confinement energy of excitons is not considerable. [8]
Lifetime of biexcitons and excitons
In solid state physics, the recombination of biexcitons (XX), which can be regarded as an entity of two weakly bound excitons (X), is often discussed in a simple way of argumentation: The recombination of any of the two excitons forming the biexciton will result in its disappearance. Therefore one would expect that the biexciton lifetime, 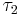 , is about half of that of the exciton,
, is about half of that of the exciton, 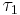 .
.
However, some elementary points of view should be taken into account. For example, a direct radiative recombination into the ground state of the crystal, allowed for the exciton state, is optically forbidden for singlet biexcitons. Furthermore, the spin structure and the Coulomb interaction of the electrons and the holes forming the excitons and the biexcitons has to be considered.
In a CdSe/ZnSe quantum dot, the lifetime of biexciton is measured as 310 ps, and that of exciton is about 290 ps. The ratio of the two lifetimes is not about 2, but about 1.
The final state of the biexciton recombination is an optically allowed (bright) exciton state. Because of exchange interaction, the excitons are split into optically allowed states (bright, 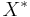 ) and optically forbidden states (dark,
) and optically forbidden states (dark, 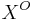 ). The spin flip time between
). The spin flip time between 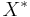 and
and 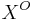 states,
states, 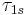 , is expected to be in the range of several ns, i.e., much longer than the bright exciton lifetime.
, is expected to be in the range of several ns, i.e., much longer than the bright exciton lifetime.
The time evolution of the probabilities for the population of the biexciton and exciton states, 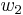 and
and 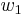 , respectively:
, respectively:
with 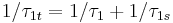 , where
, where 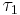 and
and 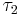 are the
are the 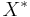 and the XX radiative recombination times, respectively.
and the XX radiative recombination times, respectively.
Solving this equation system, the X and XX dynamics can be described quantitatively. As a result, while decay of XX is monoexponential, the onset of the X line is significantly delayed, resulting in a plateaulike characteristics of the exciton decay curve. [9]
References
- ^ G. Chen et al, "Biexciton Quantum Coherence in a Single Quantum Dot", Phys. Rev. Lett., 88 (11), 117901 (2002)
- ^ Xiaoqin Li et al, "An All-Optical Quantum Gate in a Semiconductor Quantum Dot", Science, 301, 809 (2003)
- ^ Mark Fox, "Optical Properties of Solids", Oxford Univ. Press, Chap. 4 (2001)
- ^ G. Vektrais, "A new approach to the molecular biexciton theory", J. Chem. Phys., 101 (4), 3031 (1994)
- ^ S. Park et al, "Fabrication of CuCl Quantum Dots and the Size Dependence of the Biexciton Binding Energy", Journal of the Korean Physical Society, 37 (3), 309-312 (2000)
- ^ J. Liu et al, "Binding Energy of biexcitons in Two-Dimensional Semiconductors", Chin. Phys. Lett., 15 (8), 588 (1998)
- ^ T. G. Perdersen et al, "Stability and Signatures of biexcitons in Carbon nanotubes", Nanolett., 5 (2), 291 (2005)
- ^ Y. Masumoto et al, "Biexciton binding energy in CuCl quantum dots", Phys. Rev. B, 50 (24), 18658 (1994)
- ^ G. Bacher et al, "Biexciton versus exciton lifetime in a Single Semiconductor quantum dot", Phys. Rev. Lett., 83 (21), 4417 (1999)