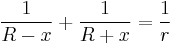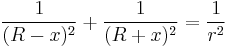Bicentric polygon
In geometry, a bicentric polygon is a tangential polygon (a polygon all of whose sides are tangent to an inner incircle) which is also cyclic — that is, inscribed in an outer circle that passes through each vertex of the polygon. All triangles and all regular polygons are bicentric. On the other hand, a rectangle with unequal sides is not bicentric, because no circle can be tangent to all four sides.
Contents |
Triangles
In a triangle, the radii r and R of the incircle and circumcircle respectively are related by the equation
where x is the distance between the centers of the circles. This is one version of Euler's triangle formula.
Bicentric quadrilaterals
Not all quadrilaterals are bicentric (having both an incircle and a circumcircle). Given two circles (one within the other) with radii R and r where 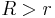 , there exists a convex quadrilateral inscribed in one of them and tangent to the other if and only if their radii satisfy
, there exists a convex quadrilateral inscribed in one of them and tangent to the other if and only if their radii satisfy
where x is the distance between their centers. This condition is known as Fuss' theorem.
Regular polygons
For all regular polygons, x=0. That is, the incircle and the circumcircle share a common center. This center is also the center of the regular polygon.
For some regular polygons which can be constructed with compass and ruler, we have the following formulas for the relation between the common edge length a, the radius r of the incircle, and the radius R of the circumcircle:
 |
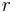 |
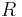 |
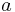 |
| 3 | 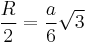 |
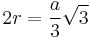 |
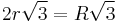 |
| 4 | 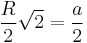 |
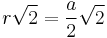 |
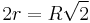 |
| 5 | 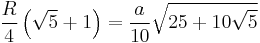 |
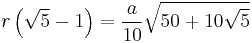 |
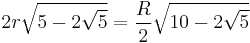 |
| 6 | 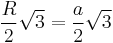 |
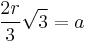 |
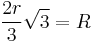 |
| 8 | 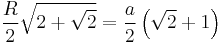 |
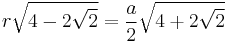 |
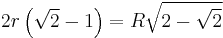 |
| 10 | 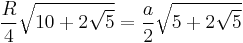 |
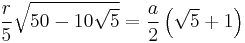 |
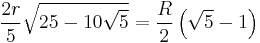 |
See also
External links
- Weisstein, Eric W., "Bicentric polygon" from MathWorld.