Bicategory

In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not (strictly) associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.

Formally, a bicategory B consists of:

objects a, b... called 0-cells;
morphisms f, g, ... with fixed source and target objects called 1-cells;
"morphisms between morphisms" ρ, σ... with fixed source and target morphisms (which should have themselves the same source and the same target), called 2-cells;

with some more structure:

given two objects a and b there is a category B(a, b) whose objects are the 1-cells and morphisms are the 2-cells, the composition in this category is called vertical composition;
given three objects a, b and c, there is a bifunctor 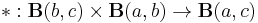$*:\mathbf{B}(b,c)\times\mathbf{B}(a,b)\to\mathbf{B}(a,c)$ called horizontal composition.

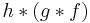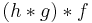The horizontal composition is required to be associative up to a natural isomorphism α between morphisms $h*(g*f)$ and $(h*g)*f$ . Some more coherence axioms, similar to those needed for monoidal categories, are moreover required to hold.

Bicategories may be considered as a weakening of the definition of 2-categories. A similar process for 3-categories leads to tricategories, and more generally to weak n-categories for n-categories.

References

J. Bénabou. "Introduction to bicategories, part I". In Reports of the Midwest Category Seminar, Lecture Notes in Mathematics 47, pages 1-77. Springer, 1967.