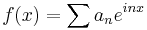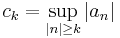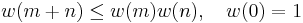Beurling algebra

In mathematics, the term Beurling algebra is used for different algebras introduced by Arne Beurling (1949), usually it is an algebra of periodic functions with Fourier series

$f(x)=\sum a_ne^{inx}$

Example We may consider the algebra of those functions f where the majorants

$c_k=\sup_{|n|\ge k} |a_n|$

of the Fourier coefficients a_n are summable. In other words

$\sum_{k\ge 0} c_k<\infty.$

Example We may consider a weight function w on $\mathbb{Z}$ such that

$w(m%2Bn)\leq w(m)w(n),\quad w(0)=1$

in which case 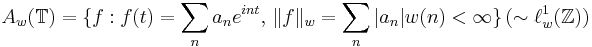$A_w(\mathbb{T}) =\{f:f(t)=\sum_na_ne^{int},\,\|f\|_w=\sum_n|a_n|w(n)<\infty\} \,(\sim\ell^1_w(\mathbb{Z}))$ is a unitary commutative Banach algebra.

These algebras are closely related to the Wiener algebra.

References

Belinsky, E.S.; Liflyand, E.R. (2001), "Beurling algebra", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b130120
Beurling, Arne (1949), "On the spectral synthesis of bounded functions", Acta Math. 81 (1): 225–238, doi:10.1007/BF02395018, MR 0027891