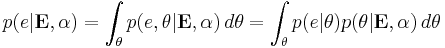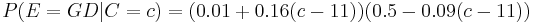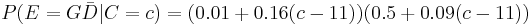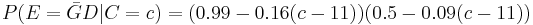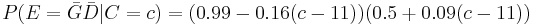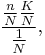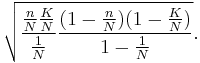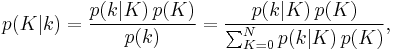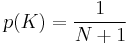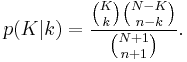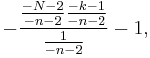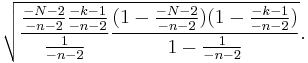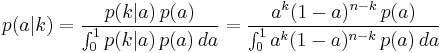Bayesian inference
In statistics, Bayesian inference is a method of statistical inference in which Bayes' theorem is used to calculate how the degree of belief in a proposition changes due to evidence. Bayesian inference is justified by the philosophy of Bayesian probability, which asserts that degrees of belief may be represented by probabilities, and that Bayes' theorem provides the rational update given the evidence[1][2].
The initial degree of belief is called the prior and the updated degree of belief the posterior.
Bayesian inference has applications in science, engineering, medicine and law.
Research has suggested that the brain may employ Bayesian inference (see Bayesian cognitive science).
Bayesian inference is used in science and engineering for model selection, see Bayes factor.
Contents |
Philosophical background
The philosophy of Bayesian probability considers the degrees of belief in a set of propositions to be rational if they obey rules equivalent to the axioms of probability. This can be justified with a Dutch book approach or with decision theory. In the analogy, events are equivalent to propositions, probabilities are equivalent to degrees of belief, and 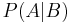 represents the degree of belief in
represents the degree of belief in  if
if  is taken to be true. For example, the degrees of belief assigned to a set of exclusive and exhaustive propositions must sum to 1.
is taken to be true. For example, the degrees of belief assigned to a set of exclusive and exhaustive propositions must sum to 1.
The language and relationships of probability theory may then be used to explore rationality. In particular, let  be any proposition and
be any proposition and  be the proposition that particular evidence will be observed. Bayes' theorem implies that
be the proposition that particular evidence will be observed. Bayes' theorem implies that 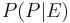 must rationally exist in a fixed relationship with beliefs known before the evidence is observed. This is the essence of Bayesian inference:
must rationally exist in a fixed relationship with beliefs known before the evidence is observed. This is the essence of Bayesian inference:
-
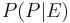 , the posterior, is the degree of belief in
, the posterior, is the degree of belief in  after
after  is observed.
is observed.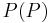 , the prior, is the degree of belief in
, the prior, is the degree of belief in  before
before  is observed.
is observed.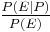 is a factor representing the impact of
is a factor representing the impact of  on the degree of belief in
on the degree of belief in  . The numerator is called the likelihood.
. The numerator is called the likelihood.
Method
General formulation
Suppose a process is generating independent and identically distributed events 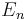 , but the probability distribution is unknown. Let the event space
, but the probability distribution is unknown. Let the event space  represent the current state of belief for this process. Each model is represented by event
represent the current state of belief for this process. Each model is represented by event 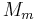 . The conditional probabilities
. The conditional probabilities 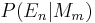 are specified to define the models.
are specified to define the models. 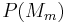 is the degree of belief in
is the degree of belief in 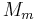 . Before the first inference step,
. Before the first inference step, 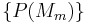 is a set of initial prior probabilities. These must sum to 1, but are otherwise arbitrary.
is a set of initial prior probabilities. These must sum to 1, but are otherwise arbitrary.
Suppose that the process is observed to generate 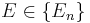 . For each
. For each 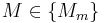 , the prior
, the prior 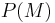 is updated to the posterior
is updated to the posterior 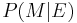 . From Bayes' theorem[3]:
. From Bayes' theorem[3]:
Upon observation of further evidence, this procedure may be repeated.
Multiple observations
For a set of independent and identically distributed observations 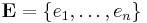 , it may be shown that repeated application of the above is equivalent to
, it may be shown that repeated application of the above is equivalent to
Where
This may speed up practical calculations.
Parametric formulation
By parametrizing the above, inference may be performed in a single step. Let the vector parameter 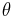 represent the set of variables to be inferred. Let
represent the set of variables to be inferred. Let 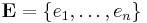 be a set of independent and identically distributed event observations, where each
be a set of independent and identically distributed event observations, where each 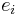 is assumed to be distributed as
is assumed to be distributed as 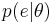 for some
for some 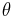 . Let the initial prior distribution over
. Let the initial prior distribution over 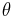 be
be 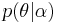 , where
, where 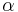 is a vector of hyperparameters. Bayes' theorem is applied to find the posterior distribution:
is a vector of hyperparameters. Bayes' theorem is applied to find the posterior distribution:
Where
Mathematical properties
Interpretation of factor
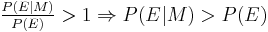 . That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in belief. If the belief does not change,
. That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in belief. If the belief does not change, 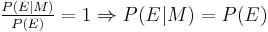 . That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.
. That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.
Cromwell's rule
If 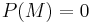 then
then 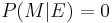 . If
. If 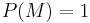 , then
, then 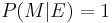 . This can be interpreted to mean that hard convictions are insensitive to counter-evidence.
. This can be interpreted to mean that hard convictions are insensitive to counter-evidence.
The former can be proved by inspection of Bayes' theorem. The latter can be proved by considering that 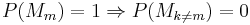 . Therefore,
. Therefore, 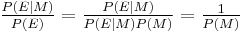 . The result now follows by substitution into Bayes' theorem.
. The result now follows by substitution into Bayes' theorem.
Asymptotic behaviour of posterior
Consider the behaviour of a belief distribution as it is updated a large number of times with independent and identically distributed trials. For sufficiently nice prior probabilities, the Bernstein-von Mises theorem gives that in the limit of infinite trials and the posterior converges to a Gaussian distribution independent of the initial prior under some conditions firstly outlined and rigorously proven by Joseph Leo Doob in 1948, namely if the random variable in consideration has a finite probability space. The more general results were obtained later by the statistician David A. Freedman who published in two seminal research papers in 1963 and 1965 when and under what circumstances the asymptotic behaviour of posterior is guaranteed. His 1963 paper treats like Doob (1949) the finite case and comes to a satisfactory conclusion. However, if the random variable has an infinite but countable probability space (i.e. corresponding to a die with infinite many faces) the 1965 paper demonstrates that for a dense subset of priors the Bernstein-von Mises theorem is not applicable. In this case there is almost surely no asymptotic convergence. Similar results were obtained in 1964 by Lorraine Schwarz. Later in the eighties and nineties Freedman and Persi Diaconis continued to work on the case of infinite countable probability spaces. We conclude that in practise, there may be insufficient trials to suppress the effects of the initial choice, and especially for large (but finite) systems the convergence might be very slow.
Conjugate priors
In paramaterized form, the prior distribution is often assumed to come from a family of distributions called conjugate priors. The usefulness of a conjugate prior is that the corresponding posterior distribution will be in the same family, and the calculation may be expressed in closed form.
Estimates of parameters and predictions
It is often desired to make a point estimate of a parameter or variable from a posterior distribution. One method of achieving this is to take the most likely value, a maximum a posteriori estimate:
Alternatively, the expectation over the whole distribution may be used. This may be viewed as more fully respecting the Bayesian philosophy, as any value with non-zero posterior probability is still believed to be potentially correct.
The predictive density of a new observation  is determined by
is determined by
Examples
Testing a hypothesis
Suppose there are two full bowls of cookies. Bowl #1 has 10 chocolate chip and 30 plain cookies, while bowl #2 has 20 of each. Our friend Fred picks a bowl at random, and then picks a cookie at random. We may assume there is no reason to believe Fred treats one bowl differently from another, likewise for the cookies. The cookie turns out to be a plain one. How probable is it that Fred picked it out of bowl #1?
Intuitively, it seems clear that the answer should be more than a half, since there are more plain cookies in bowl #1. The precise answer is given by Bayes' theorem. Let 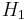 correspond to bowl #1, and
correspond to bowl #1, and 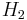 to bowl #2. It is given that the bowls are identical from Fred's point of view, thus
to bowl #2. It is given that the bowls are identical from Fred's point of view, thus  , and the two must add up to 1, so both are equal to 0.5. The event
, and the two must add up to 1, so both are equal to 0.5. The event  is the observation of a plain cookie. From the contents of the bowls, we know that
is the observation of a plain cookie. From the contents of the bowls, we know that 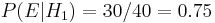 and
and 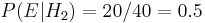 . Bayes' formula then yields
. Bayes' formula then yields
Before we observed the cookie, the probability we assigned for Fred having chosen bowl #1 was the prior probability, 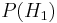 , which was 0.5. After observing the cookie, we must revise the probability to
, which was 0.5. After observing the cookie, we must revise the probability to 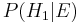 , which is 0.6.
, which is 0.6.
Evaluating a parameter
Making a prediction
An archaeologist is working at a site thought to be from the medieval period, between the 11th century to the 16th century. However, it is uncertain exactly when in this period the site was inhabited. Fragments of pottery are found, some of which are glazed and some of which are decorated. It is expected that if the site were inhabited during the early medieval period, then 1% of the pottery would be glazed and 50% of its area decorated, whereas if it had been inhabited in the late medieval period then 81% would be glazed and 5% of its area decorated. How confident can the archaeologist be in the date of inhabitation as fragments are unearthed?
The degree of belief in the continuous variable  (century) is to be calculated, with the discrete set of events
(century) is to be calculated, with the discrete set of events 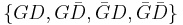 as evidence. Assuming linear variation of glaze and decoration with time, and that these variables are independent,
as evidence. Assuming linear variation of glaze and decoration with time, and that these variables are independent,
Assume a uniform prior of 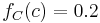 , and that trials are independent and identically distributed. When a new fragment of type
, and that trials are independent and identically distributed. When a new fragment of type  is discovered, Bayes' theorem is applied to update the degree of belief for each
is discovered, Bayes' theorem is applied to update the degree of belief for each  :
:
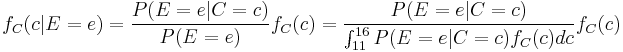
A computer simulation of the changing belief as 50 fragments are unearthed is shown on the graph. In the simulation, the site was inhabited around 1420, or 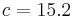 . By calculating the area under the relevant portion of the graph for 50 trials, the archaeologist can say that there is practically no chance the site was inhabited in the 11th and 12th centuries, about 1% chance that it was inhabited during the 13th century, 63% chance during the 14th century and 36% during the 15th century.Note that the Bernstein-von Mises theorem asserts here the asymptotic convergence to the "true" distribution because the probability space corresponding to the discrete set of events
. By calculating the area under the relevant portion of the graph for 50 trials, the archaeologist can say that there is practically no chance the site was inhabited in the 11th and 12th centuries, about 1% chance that it was inhabited during the 13th century, 63% chance during the 14th century and 36% during the 15th century.Note that the Bernstein-von Mises theorem asserts here the asymptotic convergence to the "true" distribution because the probability space corresponding to the discrete set of events 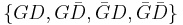 is finite (see above section on asymptotic behaviour of the posterior).
is finite (see above section on asymptotic behaviour of the posterior).
Model selection
Applications
Computer applications
Bayesian inference has applications in artificial intelligence and expert systems. Bayesian inference techniques have been a fundamental part of computerized pattern recognition techniques since the late 1950s. There is also an ever growing connection between Bayesian methods and simulation-based Monte Carlo techniques since complex models cannot be processed in closed form by a Bayesian analysis, while a graphical model structure may allow for efficient simulation algorithms like the Gibbs sampling and other Metropolis–Hastings algorithm schemes. Recently Bayesian inference has gained popularity amongst the phylogenetics community for these reasons; a number of applications allow many demographic and evolutionary parameters to be estimated simultaneously. In the areas of population genetics and dynamical systems theory approximate Bayesian computation (ABC) are also becoming increasingly popular.
As applied to statistical classification, Bayesian inference has been used in recent years to develop algorithms for identifying e-mail spam. Applications which make use of Bayesian inference for spam filtering include DSPAM, Bogofilter, SpamAssassin, SpamBayes, and Mozilla. Spam classification is treated in more detail in the article on the naive Bayes classifier.
In the courtroom
Bayesian inference can be used by jurors to coherently accumulate the evidence for and against a defendant, and to see whether, in totality, it meets their personal threshold for 'beyond a reasonable doubt'.[4][5][6] The benefit of a Bayesian approach is that it gives the juror an unbiased, rational mechanism for combining evidence. Bayes' theorem is applied successively to all evidence presented, with the posterior from one stage becoming the prior for the next. A prior probability of guilt is still required. It has been suggested that this could reasonably be the probability that a random person taken from the qualifying population is guilty. Thus, for a crime known to have been committed by an adult male living in a town containing 50,000 adult males, the appropriate initial prior might be 1/50,000.
It may be appropriate to explain Bayes' theorem to jurors in odds form, as betting odds are more widely understood than probabilities. Alternatively, a logarithmic approach, replacing multiplication with addition, might be easier for a jury to handle.
The use of Bayes' theorem by jurors is controversial. In the United Kingdom, a defence expert witness explained Bayes' theorem to the jury in R v Adams. The jury convicted, but the case went to appeal on the basis that no means of accumulating evidence had been provided for jurors who did not wish to use Bayes' theorem. The Court of Appeal upheld the conviction, but it also gave the opinion that "To introduce Bayes' Theorem, or any similar method, into a criminal trial plunges the jury into inappropriate and unnecessary realms of theory and complexity, deflecting them from their proper task."
Gardner-Medwin[7] argues that the criterion on which a verdict in a criminal trial should be based is not the probability of guilt, but rather the probability of the evidence, given that the defendant is innocent (akin to a frequentist p-value). He argues that if the posterior probability of guilt is to be computed by Bayes' theorem, the prior probability of guilt must be known. This will depend on the incidence of the crime, which is an unusual piece of evidence to consider in a criminal trial. Consider the following three propositions:
- A The known facts and testimony could have arisen if the defendant is guilty
- B The known facts and testimony could have arisen if the defendant is innocent
- C The defendant is guilty.
Gardner-Medwin argues that the jury should believe both A and not-B in order to convict. A and not-B implies the truth of C, but the reverse is not true. It is possible that B and C are both true, but in this case he argues that a jury should acquit, even though they know that they will be letting some guilty people go free. See also Lindley's paradox.
Other
- The scientific method is sometimes interpreted as an application of Bayesian inference. In this view, Bayes' rule guides (or should guide) the updating of probabilities about hypotheses conditional on new observations or experiments.[8]
- In March 2011, English Heritage reported the successful outcome of a research project by archaeologists at Cardiff University, which demonstrated the possibility of using Bayesian inference to more accurately date prehistoric remains.[9]
- Bayesian search theory is used to search for lost objects.
- Bayesian inference in phylogeny
- Bayesian tool for methylation analysis
Distribution of a parameter of the hypergeometric distribution
Consider a sample of  marbles drawn from an urn containing
marbles drawn from an urn containing  marbles.
marbles.
If the number of white marbles in the urn is known to be equal to  , then the probability that the number of white marbles in the sample is equal to
, then the probability that the number of white marbles in the sample is equal to  , is
, is
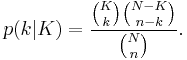 .
.
The mean number of white marbles in the sample is
and the standard deviation is
An interesting situation is when the number of white marbles in the sample is known, and the number of white marbles in the urn is unknown.
If the number of white marbles in the sample is equal to  , then the degree of belief that the number of white marbles in the urn is equal to
, then the degree of belief that the number of white marbles in the urn is equal to  , is
, is
where 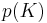 is the probability that the number of white marbles in the urn is equal to
is the probability that the number of white marbles in the urn is equal to  , that is before observing the number of white marbles in the sample, and
, that is before observing the number of white marbles in the sample, and 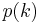 is the probability that the number of white marbles in the sample is equal to
is the probability that the number of white marbles in the sample is equal to  , without knowing the number of white marbles in the urn.
, without knowing the number of white marbles in the urn.
Assume now that all the possibilities are considered equally likely in advance,
for 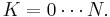
Then the degree of belief that the number of white marbles in the urn is equal to  , is
, is
The mean number of white marbles in the urn is
and the standard deviation is
These two formulas regarding the number of white marbles in the urn emerge from the simpler formulas regarding the number of white marbles in the sample by the substitution 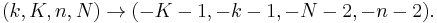
The limiting cases for 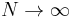 ,
, 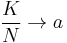 are the binomial distribution and the beta distribution, see below.
are the binomial distribution and the beta distribution, see below.
Posterior distribution of the binomial parameter
The problem considered by Bayes in Proposition 9 of his essay is the posterior distribution for the parameter of the binomial distribution.
Consider 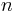 Bernoulli trials.
Bernoulli trials.
If the success probability is equal to 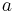 , then the conditional probability of observing
, then the conditional probability of observing 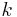 successes is the (discrete) binomial distribution function
successes is the (discrete) binomial distribution function 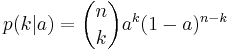 . The mean value of
. The mean value of  is
is 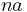 , and the standard deviation is
, and the standard deviation is 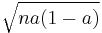 . The mean value of
. The mean value of 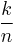 is
is 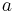 , and the standard deviation is
, and the standard deviation is 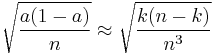 .
.
In the more realistic situation when 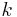 is known and
is known and 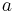 is unknown,
is unknown, 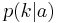 is a likelihood function of
is a likelihood function of 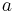 . The posterior probability distribution function of
. The posterior probability distribution function of 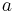 , after observing
, after observing 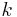 , is
, is
where a prior probability distribution function, 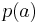 , is available to express what was known about
, is available to express what was known about 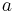 before observing
before observing 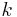 .
.
Assume now that the prior distribution is the continuous uniform distribution, 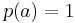 for
for 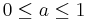 .
.
Then the posterior distribution 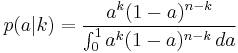 is the beta distribution,
is the beta distribution, 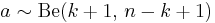 . The mean value of
. The mean value of 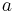 is
is 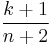 , rather than
, rather than 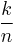 , and the standard deviation is
, and the standard deviation is 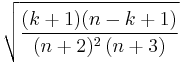 , rather than
, rather than 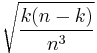 .
.
If the prior distribution is 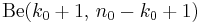 , then the posterior distribution is
, then the posterior distribution is 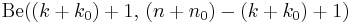 . So the beta distribution is a conjugate prior.
. So the beta distribution is a conjugate prior.
What is "Bayesian" about Proposition 9 is that Bayes presented it as a probability for the parameter  . That is, not only can one compute probabilities for experimental outcomes, but also for the parameter which governs them, and the same algebra is used to make inferences of either kind. Interestingly, Bayes actually states his question in a way that might make the idea of assigning a probability distribution to a parameter palatable to a frequentist. He supposes that a billiard ball is thrown at random onto a billiard table, and that the probabilities p and q are the probabilities that subsequent billiard balls will fall above or below the first ball. By making the binomial parameter
. That is, not only can one compute probabilities for experimental outcomes, but also for the parameter which governs them, and the same algebra is used to make inferences of either kind. Interestingly, Bayes actually states his question in a way that might make the idea of assigning a probability distribution to a parameter palatable to a frequentist. He supposes that a billiard ball is thrown at random onto a billiard table, and that the probabilities p and q are the probabilities that subsequent billiard balls will fall above or below the first ball. By making the binomial parameter 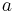 depend on a random event, he cleverly escapes a philosophical quagmire that was an issue he most likely was not even aware of.
depend on a random event, he cleverly escapes a philosophical quagmire that was an issue he most likely was not even aware of.
History
The term Bayesian refers to Thomas Bayes (1702–1761), who proved a special case of what is now called Bayes' theorem. However, it was Pierre-Simon Laplace (1749–1827) who introduced a general version of the theorem and used it to approach problems in celestial mechanics, medical statistics, reliability, and jurisprudence.[10] Early Bayesian inference, which used uniform priors following Laplace's principle of insufficient reason, was called "inverse probability" (because it infers backwards from observations to parameters, or from effects to causes[11]). After the 1920s, "inverse probability" was largely supplanted by a collection of methods that came to be called frequentist statistics.[11]
In the 20th century, the ideas of Laplace were further developed in two different directions, giving rise to objective and subjective currents in Bayesian practice. In the objectivist stream, the statistical analysis depends on only the model assumed and the data analysed.[12] No subjective decisions need to be involved. In contrast, "subjectivist" statisticians deny the possibility of fully objective analysis for the general case.
In the 1980s, there was a dramatic growth in research and applications of Bayesian methods, mostly attributed to the discovery of Markov chain Monte Carlo methods, which removed many of the computational problems, and an increasing interest in nonstandard, complex applications.[13] Despite growth of Bayesian research, most undergraduate teaching is still based on frequentist statistics.[14] Nonetheless, Bayesian methods are widely accepted and used, such as for example in the field of machine learning.[15]
Notes
- ^ Stanford encyclopedia of philosophy; Bayesian Epistemology; http://plato.stanford.edu/entries/epistemology-bayesian
- ^ Gillies, Donald (2000); "Philosophical Theories of Probability"; Routledge; Chapter 4 "The subjective theory"
- ^ Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Rubin, Donald B. (2003). Bayesian Data Analysis, Second Edition. Boca Raton, FL: Chapman and Hall/CRC. ISBN 1-584-88388-X.
- ^ Dawid, A.P. and Mortera, J. (1996) "Coherent analysis of forensic identification evidence". Journal of the Royal Statistical Society, Series B, 58,425–443.
- ^ Foreman, L.A; Smith, A.F.M. and Evett, I.W. (1997). "Bayesian analysis of deoxyribonucleic acid profiling data in forensic identification applications (with discussion)". Journal of the Royal Statistical Society, Series A, 160, 429–469.
- ^ Robertson, B. and Vignaux, G.A. (1995) Interpreting Evidence: Evaluating Forensic Science in the Courtroom. John Wiley and Sons. Chichester. ISBN 978-0-471-96026-3
- ^ Gardner-Medwin, A. (2005) "What probability should the jury address?". Significance, 2 (1), March 2005
- ^ Howson & Urbach (2005), Jaynes (2003)
- ^ Pitts, Mike (March 2011). "Gathering Time: why the completion of an exciting new research project could change the way we think about prehistoric eras around the world". Heritage Today: 24–7.
- ^ Stephen M. Stigler (1986) The history of statistics. Harvard University press. Chapter 3.
- ^ a b Stephen. E. Fienberg, (2006) "When did Bayesian Inference become "Bayesian"? Bayesian Analysis, 1 (1), 1–40. See page 5.
- ^ JM. Bernardo (2005), "Reference analysis", Handbook of statistics, 25, 17–90
- ^ Wolpert, RL. (2004) A conversation with James O. Berger, Statistical science, 9, 205–218
- ^ José M. Bernardo (2006) A Bayesian mathematical statistics prior. ICOTS-7
- ^ Bishop, C.M. (2007) Pattern Recognition and Machine Learning. Springer, 2007
References
- Bickel, Peter J. and Doksum, Kjell A. (2001). Mathematical Statistics, Volume 1: Basic and Selected Topics (Second (updated printing 2007) ed.). Pearson Prentice–Hall. ISBN 013850363X.
- Box, G.E.P. and Tiao, G.C. (1973) Bayesian Inference in Statistical Analysis, Wiley, ISBN 0-471-57428-7
- Edwards, Ward (1968). "Conservatism in Human Information Processing". In Kleinmuntz, B. Formal Representation of Human Judgment. Wiley.
- Edwards, Ward (1982). "Conservatism in Human Information Processing (excerpted)". In Daniel Kahneman, Paul Slovic and Amos Tversky. Judgment under uncertainty: Heuristics and biases. Cambridge University Press.
- Jaynes E.T. (2003) Probability Theory: The Logic of Science, CUP. ISBN 978-0-521-59271-0 (Link to Fragmentary Edition of March 1996).
- Howson, C. and Urbach, P. (2005). Scientific Reasoning: the Bayesian Approach (3rd ed.). Open Court Publishing Company. ISBN 978-0812695786.
- Phillips, L.D.; Edwards, W. (October 2008). "Chapter 6: Conservatism in a simple probability inference task (Journal of Experimental Psychology (1966) 72: 346-354)". In Jie W. Weiss and David J. Weiss. A Science of Decision Making:The Legacy of Ward Edwards. Oxford University Press. pp. 536. ISBN 9780195322989.
Further reading
Elementary
The following books are listed in ascending order of probabilistic sophistication:
- Colin Howson and Peter Urbach (2005). Scientific Reasoning: the Bayesian Approach (3rd ed.). Open Court Publishing Company. ISBN 978-0812695786.
- Berry, Donald A. (1996). Statistics: A Bayesian Perspective. Duxbury. ISBN 0534234763.
- Morris H. DeGroot and Mark J. Schervish (2002). Probability and Statistics (third ed.). Addison-Wesley. ISBN 9780201524888.
- Bolstad, William M. (2007) Introduction to Bayesian Statistics: Second Edition, John Wiley ISBN 0-471-27020-2
- Winkler, Robert L, Introduction to Bayesian Inference and Decision, 2nd Edition (2003) ISBN 0-9647938-4-9
- Lee, Peter M. Bayesian Statistics: An Introduction. Second Edition. (1997). ISBN 0-340-67785-6.
- Bayesian Methods for Data Analysis, Third Edition. Boca Raton, FL: Chapman and Hall/CRC. 2008. ISBN 1-584-88697-8.
- Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Rubin, Donald B. (2003). Bayesian Data Analysis, Second Edition. Boca Raton, FL: Chapman and Hall/CRC. ISBN 1-584-88388-X.
- Pole, Andy, West, Mike and Harrison, P. Jeff. Applied Bayesian Forecasting and Time Series Analysis, Chapman-Hall/Taylor Francis, 1994
Intermediate or advanced
- Berger, James O (1985). Statistical Decision Theory and Bayesian Analysis. Springer Series in Statistics (Second ed.). Springer-Verlag. ISBN 0-387-96098-8.
- Bayesian Theory. Wiley. 1994.
- Bolstad, William M. (2010) Understanding Computational Bayesian Statistics, John Wiley ISBN 0-470-04609-8
- Bretthorst, G. Larry, 1988, Bayesian Spectrum Analysis and Parameter Estimation in Lecture Notes in Statistics, 48, Springer-Verlag, New York, New York
- DeGroot, Morris H., Optimal Statistical Decisions. Wiley Classics Library. 2004. (Originally published (1970) by McGraw-Hill.) ISBN 0-471-68029-X.
- Jaynes, E.T. (1998) Probability Theory: The Logic of Science.
- David MacKay (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press. (On-line)
- O'Hagan, A. and Forster, J. (2003) Kendall's Advanced Theory of Statistics, Volume 2B: Bayesian Inference. Arnold, New York. ISBN 0-340-52922-9.
- Robert, Christian P (2001). The Bayesian Choice – A Decision-Theoretic Motivation (second ed.). Springer. ISBN 0387942963.
- Glenn Shafer and Pearl, Judea, eds. (1988) Probabilistic Reasoning in Intelligent Systems, San Mateo, CA: Morgan Kaufmann.
- West, Mike, and Harrison, P. Jeff, Bayesian Forecasting and Dynamic Models, Springer-Verlag, 1997 (2nd ed.)
External links
- Bayesian Statistics summary from Scholarpedia.
- A nice on-line introductory tutorial to Bayesian probability from Queen Mary University of London
- An Intuitive Explanation of Bayesian Reasoning "Bayes' Theorem for the curious and bewildered; an excruciatingly gentle introduction by Eliezer Yudkowsky"
- Paul Graham. "A Plan for Spam" (exposition of a popular approach for spam classification)
- Commentary on Regina versus Adams
- Mathematical notes on Bayesian statistics and Markov chain Monte Carlo
- Bayesian Rating/Ranking How to implement Bayes' Theorem for online rating and ranking systems
- Bayesian reading list, categorized and annotated. Designed for cognitive science; maintained by Tom Griffiths.
- Stanford Encyclopedia of Philosophy: Inductive Logic a comprehensive Bayesian treatment of Inductive Logic and Confirmation Theory
- Bayesian Confirmation Theory An extensive presentation of Bayesian Confirmation Theory
- What is Bayesian Learning?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
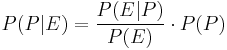
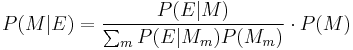
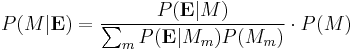
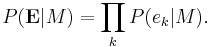
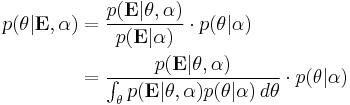
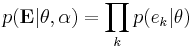
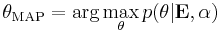
![\tilde \theta = \mathbb{E}[\theta] = \int_\theta \theta \, p(\theta|\mathbf{E},\alpha) \, d\theta](/2012-wikipedia_en_all_nopic_01_2012/I/bfef6dfd9101772e297cf6b48331a787.png)