Pointed set

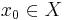In mathematics, a pointed set is a set $X$ with a distinguished element $x_0\in X$ , which is called the basepoint. Maps of pointed sets (based maps) are those functions that map one basepoint to another, i.e. a map 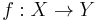$f�: X \to Y$ such that 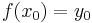$f(x_0) = y_0$ . This is usually denoted

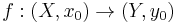$f�: (X, x_0) \to (Y, y_0)$ .

Pointed sets may be regarded as a rather simple algebraic structure. In the sense of universal algebra, they are structures with a single nullary operation which picks out the basepoint.

The class of all pointed sets together with the class of all based maps form a category.

A pointed set may be seen as a pointed space under the discrete topology or as a vector space over the field with one element.

References

Grégory Berhuy (2010). An Introduction to Galois Cohomology and Its Applications. London Mathematical Society Lecture Note Series. 377. Cambridge University Press. p. 34. ISBN 0521738660.