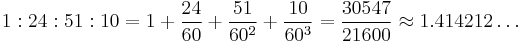Sexagesimal

Numeral systems by culture
Hindu-Arabic numerals
Western Arabic (Hindu numerals) Eastern Arabic Indian family Tamil	Burmese Khmer Lao Mongolian Thai
East Asian numerals
Chinese Japanese Suzhou	Korean Vietnamese Counting rods
Alphabetic numerals
Abjad Armenian Āryabhaṭa Cyrillic	Ge'ez Greek Georgian Hebrew
Other systems
Aegean Attic Babylonian Brahmi Egyptian Etruscan Inuit	Kharosthi Mayan Quipu Roman Sumerian Urnfield
List of numeral system topics
Positional systems by base
Decimal (10)
2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64
Non-positional system
Unary numeral system (Base 1)
List of numeral systems

Sexagesimal (base 60) is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, it was passed down to the ancient Babylonians, and it is still used — in a modified form — for measuring time, angles, and the geographic coordinates that are angles.

The number 60, a highly composite number, has twelve factors, namely { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 } of which two, three, and five are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, six minutes, five minutes, etc. Sixty is the smallest number that is evenly divisible by every number from one to six. This is because 60 = 1 × 60 = 4 × 3 × 5 = 2 × 6 × 5.

In this article, all sexagesimal digits are represented as decimal numbers, except where otherwise noted. [For example, 10 means ten and 60 means sixty.]

1 Origin
2 Usage
3 Fractions
4 Examples
5 See also
6 References
7 Additional reading

Origin

It is possible to count to 12 with your thumb acting as a pointer, touching each finger bone in turn. A traditional finger counting system still in use in many regions of Asia works in this way, and could help to explain the occurrence of numeral systems based on 12 and 60 besides those based on 10, 20 and 5. In this system, the one (usually right) hand counts repeatedly to 12, displaying the number of iterations on the other (usually left), until five dozens, i. e. the 60, are full.^[1]^[2]

According to Neugebauer, the origins of the sixty-count was through a count of three twenties. The precursor to the later six-ten alternation was through symbols for the sixths, (ie 1/6, 2/6, 3/6, 4/6, 5/6), coupled with decimal numbers, lead to the same three-score count, and also to the division-system that the Sumerians were famous for. In normal use, numbers were a hap-hazard collection of units, tens, sixties, and hundreds. A number like 192, would be expressed uniformly in the tables as 3A2 (A as the symbol for the '10', would in the surrounding text, be given as XIxii ie, hundred (big 10), sixty (big 1), ten (little 10), two (little 1's). ^[3]

Usage

Babylonian mathematics

The sexagesimal system as used in ancient Mesopotamia was not a pure base-60 system, in the sense that it did not use 60 distinct symbols for its digits. Instead, the cuneiform digits used ten as a sub-base in the fashion of a sign-value notation: a sexagesimal digit was composed of a group of narrow, wedge-shaped marks representing units up to nine (Y, YY, YYY, YYYY, ... YYYYYYYYY) and a group of wide, wedge-shaped marks representing up to five tens (<, <<, <<<, <<<<, <<<<<). The value of the digit was the sum of the values of its component parts:

Numbers larger than 59 were indicated by multiple symbol blocks of this form in place value notation.

Because there was no symbol for zero in Sumerian or early Babylonian numbering systems, it is not always immediately obvious how a number should be interpreted, and its true value must sometimes have been determined by its context. Later Babylonian texts used a placeholder to represent zero, but only in the medial positions, and not on the right-hand side of the number, as we do in numbers like 13,200.

Other historical usages

In the Chinese calendar, a sexagenary cycle is commonly used, in which days or years are named by positions in a sequence of ten stems and in another sequence of 12 branches. The same stem and branch repeat every 60 steps through this cycle.

Ptolemy's Almagest, a treatise on mathematical astronomy written in the second century AD, uses base 60 for all numerals. In particular, his table of chords, which was essentially the only extensive trigonometric table for more than a millennium, is in base 60.

Base-60 number systems have also been used in some other cultures that are unrelated to the Sumerians, for by example the Ekagi people of Western New Guinea.^[4]^[5]

Modern usage

Unlike most other numeral systems, sexagesimal is not used so much in modern times as a means for general computations, or in logic, but rather, it is used in measuring angles, geographic coordinates, and time.

One hour of time is divided into 60 minutes, and one minute is divided into 60 seconds. Thus, a measurement of time such as "3:23:17" (three hours, 23 minutes, and 17 seconds) can be interpreted as a sexagesimal number, meaning 3×60² + 23×60¹ + 17×60⁰. As with the ancient Babylonian sexagesimal system, however, each of the three sexagesimal digits in this number (3, 23, and 17) is written using the decimal system.

Similarly, the practical unit of angular measure is the degree, of which there are 360 in a circle. There are 60 minutes of arc in a degree, and 60 arcseconds in a minute.

In some usage systems, each position past the sexagesimal point was numbered, using Latin or French roots: prime or primus, seconde or secundus, tierce, quatre, quinte, etc. To this day we call the second-order part of an hour or of a degree a "second". Until at least the 18th century, 1/60 of a second was called a "tierce" or "third".^[6]^[7]

In popular culture

In Robert A. Heinlein's science fiction novel, Methuselah's Children, Heinlein described a future race of super-intelligent humans which uses a base-60 number system and alphabet of exactly sixty ideographs.

In Stel Pavlou's novel Decipher, this number system is the center of focus, as the buckyball carbon element is used in the book to store data, and only base 60 is found to be able to be successfully understood by the computers used in it. At least one popular book^[8] uses the spelling "sexigesimal" instead of "sexagesimal," with the latter being the more common spelling of the word.

Book VIII of Plato's Republic involves an allegory of marriage centered on the number 60⁴ = 12,960,000 and its divisors. This number has the particularly simple sexagesimal representation 1:0:0:0:0. Later scholars have invoked both Babylonian mathematics and music theory in an attempt to explain this passage.^[9]

Fractions

In the sexagesimal system, any fraction in which the denominator is a regular number (having only 2, 3, and 5 in its prime factorization) may be expressed exactly.^[10] The table below shows the sexagesimal representation of all fractions of this type in which the denominator is less than 60. The sexagesimal values in this table may be interpreted as giving the number of minutes and seconds in a given fraction of an hour; for instance, 1/9 of an hour is 6 minutes and 40 seconds. However, the representation of these fractions as sexagesimal numbers does not depend on such an interpretation.


Fraction:	1/2	1/3	1/4	1/5	1/6	1/8	1/9	1/10
Sexagesimal:	30	20	15	12	10	7:30	6:40	6
Fraction:	1/12	1/15	1/16	1/18	1/20	1/24	1/25	1/27
Sexagesimal:	5	4	3:45	3:20	3	2:30	2:24	2:13:20

Fraction:	1/30	1/32	1/36	1/40	1/45	1/48	1/50	1/54
Sexagesimal:	2	1:52:30	1:40	1:30	1:20	1:15	1:12	1:6:40

However numbers that are not regular form more complicated repeating fractions. For example:

1/7 = 0:8:34:17:8:34:17 ... (with the sequence of sexagesimal digits 8:34:17 repeating infinitely often).

The fact in arithmetic that the two numbers that are adjacent to 60, namely 59 and 61, are both prime numbers implies that simple repeating fractions that repeat with a period of one or two sexagesimal digits can only have 59 or 61 as their denominators, and that other non-regular primes have fractions that repeat with a longer period.

Examples

The square root of 2, the length of the diagonal of a unit square, was approximated by the Babylonians of the Old Babylonian Period (1900 BC – 1650 BC) as

$1:24:51:10=1%2B\frac{24}{60}%2B\frac{51}{60^2}%2B\frac{10}{60^3}=\frac{30547}{21600}\approx 1.414212\ldots$ ^[11]

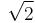Because $\sqrt{2}$ is an irrational number, it cannot be expressed exactly in sexagesimal numbers, but its sexagesimal expansion does begin 1 : 24 : 51 : 10 : 7 : 46 : 6 : 4 : 44 ...

The length of the tropical year in Neo-Babylonian astronomy (see Hipparchus), 365.24579... days, can be expressed in sexagesimal as 6:5:14:44:51 (6×60 ＋ 5 + 14/60 + 44/60² + 51/60³) days. The average length of a year in the Gregorian calendar is exactly 6 : 5 : 14 : 33 in the same notation because the values 14 and 33 were the first two values for the tropical year from the Alfonsine tables, which were in sexagesimal notation.

The value of π as used by the Greek mathematican and scientist Claudius Ptolemaeus (Ptolemy) was 3.141666... ≈ 377/120 = 3:8:30 = 3 + 8/60 + 30/60². Jamshīd al-Kāshī, a 15th-century Persian mathematician, calculated π in sexagesimal numbers to an accuracy of nine sexagesimal digits.^[12]

References

^ Ifrah, Georges (2000), The Universal History of Numbers: From prehistory to the invention of the computer., John Wiley and Sons, ISBN 0-471-39340-1 . Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk.
^ Macey, Samuel L. (1989). The Dynamics of Progress: Time, Method, and Measure. Atlanta, Georgia: University of Georgia Press. pp. 92. ISBN 978-0-8203-3796-8. http://books.google.com/books?id=xlzCWmXguwsC&pg=PA92&lpg=PA92.
^ Neugebauer, O. (1969). The Exact Sciences In Antiquity. Dover. pp. 239. ISBN 0-486-22332-9.
^ Bowers, Nancy (1977), "Kapauku numeration: Reckoning, racism, scholarship, and Melanesian counting systems", Journal of the Polynesian Society 86 (1): 105–116., http://www.ethnomath.org/resources/bowers1977.pdf
^ Lean, Glendon Angove (1992), Counting Systems of Papua New Guinea and Oceania, Ph.D. thesis, Papua New Guinea University of Technology, http://www.uog.ac.pg/glec/thesis/thesis.htm . See especially chapter 4.
^ Wade, Nicholas (1998), A natural history of vision, MIT Press, p. 193, ISBN 9780262731294
^ Lewis, Robert E. (1952), Middle English Dictionary, University of Michigan Press, p. 231, ISBN 9780472012121
^ Mlodinow, Leonard: "Euclid's Window", page 10. The Free Press, 2001
^ Barton, George A. (1908), "On the Babylonian origin of Plato's nuptial number", Journal of the American Oriental Society (Journal of the American Oriental Society, Vol. 29) 29: 210–219, doi:10.2307/592627, JSTOR 592627 . McClain, Ernest G.; Plato, (1974), "Musical “Marriages” in Plato's “Republic”", Journal of Music Theory (Journal of Music Theory, Vol. 18, No. 2) 18 (2): 242–272, doi:10.2307/843638, JSTOR 843638
^ Neugebauer, Otto E. (1955), Astronomical Cuneiform Texts, London: Lund Humphries
^ YBC 7289 clay tablet
^ Youschkevitch, Adolf P., "Al-Kashi", in Rosenfeld, Boris A., Dictionary of Scientific Biography, p. 256 .

Additional reading

Ifrah, Georges (1999), The Universal History of Numbers: From Prehistory to the Invention of the Computer, Wiley, ISBN 0-471-37568-3 .
Nissen, Hans J.; Damerow, P.; Englund, R. (1993), Archaic Bookkeeping, University of Chicago Press, ISBN 0-226-58659-6 .