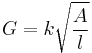Barlow's law
Barlow's law was an incorrect physical law proposed by Peter Barlow in 1824 to describe the ability of wires to conduct electricity.[1] It said that the conductance of a wire varies inversely with the square root of its length and directly with the square root of its cross-sectional area, or:
where G is conductance, l is the length of the wire, A is the cross-sectional area of the wire, and k is a constant specific to the material of the wire.
In 1827, Georg Ohm proposed a different law, stating that the resistance of a wire varies directly with its length and inversely with its cross-sectional area. Experiments eventually proved Ohm's law correct and Barlow's false.
Barlow undertook his experiments with the aim of determining whether long-distance telegraphy was feasible, and believed he proved that it was not.[2] The publication of Barlow's law delayed research into telegraphy for several years, until Joseph Henry and Philip Ten Eyck disproved it in 1831.
References
- ^ Aligny, Henry Ferdinand Quarré; Alfred Huet, F. Geyler, C. Lepainteur (1870). Report on Mining and the Mechanical Preparation of Ores. United States of America Government Printing Office. pp. 9–10.
- ^ Schiffer, Michael (2008). Power Struggles: Scientific Authority and the Creation of Practical Electricity Before Edison. MIT Press. pp. 43–45. ISBN 0262195828. "Barlow's law had devastating implications for anyone who might have considered building an electromagnetic telegraph. Transmitted over a long distance, the current would be undetectable. Indeed, Barlow reported, 'I found such a sensible diminution with only 200 feet of wire, as at once to convince me of the impracticability of the scheme.'"