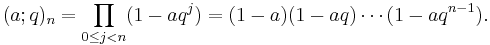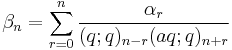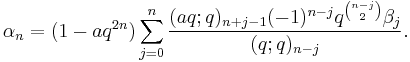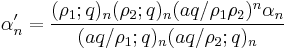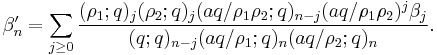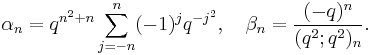Bailey pair

"Bailey's method" redirects here, for the root finding algorithm, see Bailey's method (root finding).

In mathematics, a Bailey pair is a pair of sequences satisfying certain relations, and a Bailey chain is a sequence of Bailey pairs. Bailey pairs were introduced by W. N. Bailey (1947, 1948) while studying the second proof Rogers (1917) of the Rogers-Ramanujan identities, and Bailey chains were introduced by Andrews (1984).

1 Definition
2 Bailey's lemma
3 Examples
4 References

Definition

The q-Pochhammer symbols 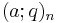$(a;q)_n$ are defined as:

$(a;q)_n = \prod_{0\le j<n}(1-aq^j) = (1-a)(1-aq)\cdots(1-aq^{n-1}).$

A pair of sequences (α_n,β_n) is called a Bailey pair if they are related by

$\beta_n=\sum_{r=0}^n\frac{\alpha_r}{(q;q)_{n-r}(aq;q)_{n%2Br}}$

or equivalently

$\alpha_n = (1-aq^{2n})\sum_{j=0}^n\frac{(aq;q)_{n%2Bj-1}(-1)^{n-j}q^{n-j\choose 2}\beta_j}{(q;q)_{n-j}}.$

Bailey's lemma

Bailey's lemma states that if (α_n,β_n) is a Bailey pair, then so is (α'_n,β'_n) where

$\alpha^\prime_n= \frac{(\rho_1;q)_n(\rho_2;q)_n(aq/\rho_1\rho_2)^n\alpha_n}{(aq/\rho_1;q)_n(aq/\rho_2;q)_n}$

$\beta^\prime_n = \sum_{j\ge0}\frac{(\rho_1;q)_j(\rho_2;q)_j(aq/\rho_1\rho_2;q)_{n-j}(aq/\rho_1\rho_2)^j\beta_j}{(q;q)_{n-j}(aq/\rho_1;q)_n(aq/\rho_2;q)_n}.$

In other words, given one Bailey pair, one can construct a second using the formulas above. This process can be iterated to produce an infinite sequence of Bailey pairs, called a Bailey chain.

Examples

An example of a Bailey pair is given by (Andrews, Askey & Roy 1999, p. 590)

$\alpha_n = q^{n^2%2Bn}\sum_{j=-n}^n(-1)^jq^{-j^2}, \quad \beta_n = \frac{(-q)^n}{(q^2;q^2)_n}.$

L. J. Slater (1952) gave a list of 130 examples related to Bailey pairs.

References

Andrews, George E. (1984), "Multiple series Rogers-Ramanujan type identities", Pacific Journal of Mathematics 114 (2): 267–283, ISSN 0030-8730, MR 757501, http://projecteuclid.org/euclid.pjm/1102708707
Andrews, George E.; Askey, Richard; Roy, Ranjan (1999), Special functions, Encyclopedia of Mathematics and its Applications, 71, Cambridge University Press, ISBN 978-0-521-62321-6; 978-0-521-78988-2, MR 1688958
Bailey, W. N. (1947), "Some identities in combinatory analysis", Proceedings of the London Mathematical Society. Second Series 49 (6): 421–425, doi:10.1112/plms/s2-49.6.421, ISSN 0024-6115, MR 0022816
Bailey, W. N. (1948), "Identities of the Rogers-Ramanujan Type", Proc. London Math. Soc. s2-50 (1): 1–10, doi:10.1112/plms/s2-50.1.1
Paule, Peter, The Concept of Bailey Chains, http://www.emis.de/journals/SLC/opapers/s18paule.pdf
Slater, L. J. (1952), "Further identities of the Rogers-Ramanujan type", Proceedings of the London Mathematical Society. Second Series 54 (2): 147–167, doi:10.1112/plms/s2-54.2.147, ISSN 0024-6115, MR 0049225
Warnaar, S. Ole (2001), "50 years of Bailey's lemma", Algebraic combinatorics and applications (Gössweinstein, 1999), Berlin, New York: Springer-Verlag, pp. 333–347, MR 1851961, http://www.maths.uq.edu.au/~uqowarna/pubs/Bailey50.pdf

Bailey pair

Contents

Definition

Bailey's lemma

Examples

References